Notes
four squares in a circle solution
Four Squares in a Circle
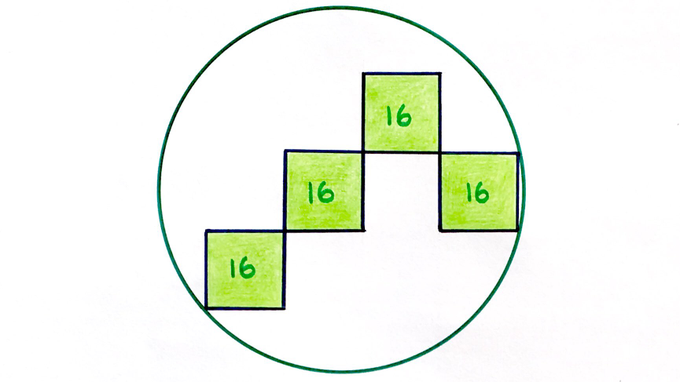
What’s the area of the circle?
Solution by Properties of Chords, Similar Triangles, and Pythagoras' Theorem
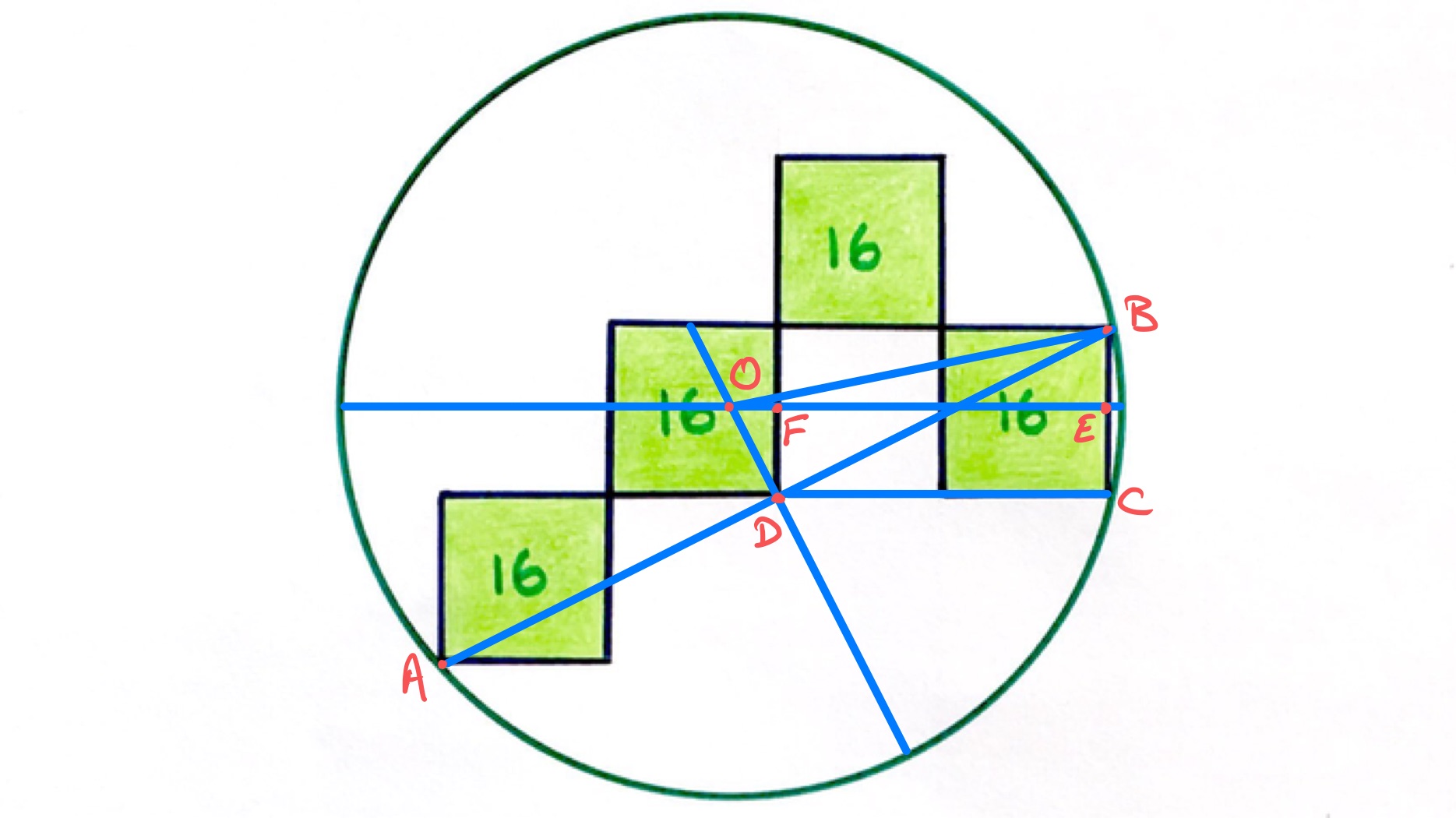
In the above diagram, is the centre of the circle, is the midpoint of , and is the midpoint of and is also the corner of the second square.
The perpendicular bisector of a chord passes through the centre of the circle. So the centre lies where the horizontal line through meets the perpendicular line to through . The triangle is therefore similar to triangle , so the length of is twice that of . Since is half the side of a square, has length and so has length . Therefore has length . The length of is . Let be the radius of the circle, then this is the length of . Applying Pythagoras' theorem to triangle shows that:
The area of the circle is therefore .