Notes
four squares ii solution
Solution to the Four Squares II Puzzle
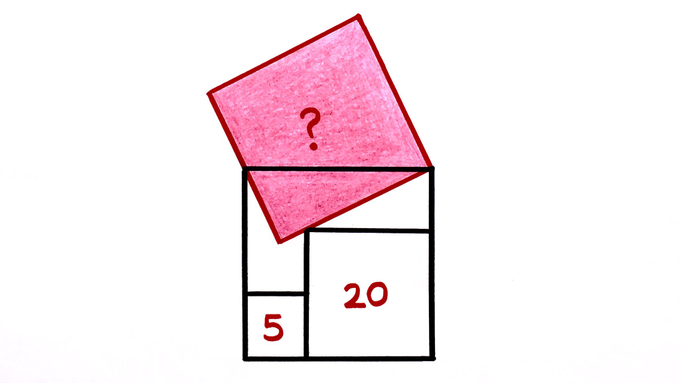
Four squares. What’s the shaded area?
Solution by Dissection and Similar Triangles
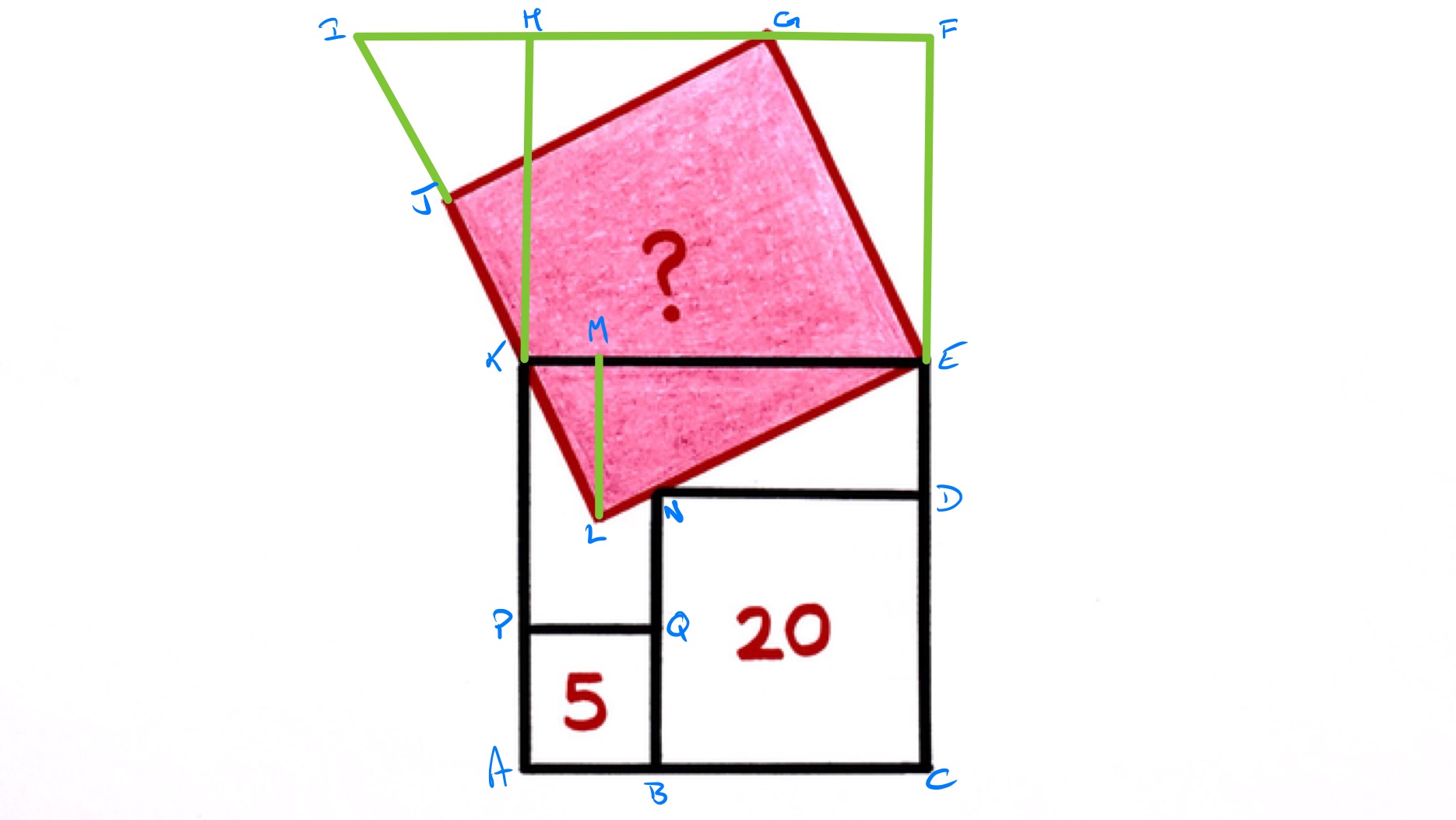
With the points labelled as in the above diagram, the shaded region has the same area as that of rectangle . This can be seen by dissection, since triangles and are congruent, and then triangles and are also congruent.
Triangle is also congruent to , so the length of is the same as that of . It is also similar to triangle . The squares and have area scale factor , so have length scale factor , meaning that is twice the length of . So is twice the length of . By similarity, then, is twice the length of which is twice the length of , so is ths of .
The area of is therefore ths of the area of a square with side length , but such as square is and this has area . So the shaded area is .