Notes
four squares around a quadrilateral solution
Four Squares Around a Quadrilateral
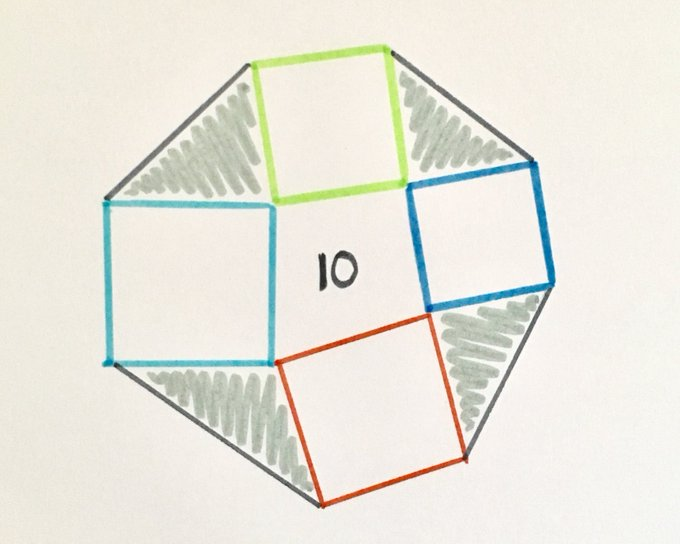
The four squares enclose a quadrilateral of area . What’s the total shaded area?
Solution by Area of a Triangle
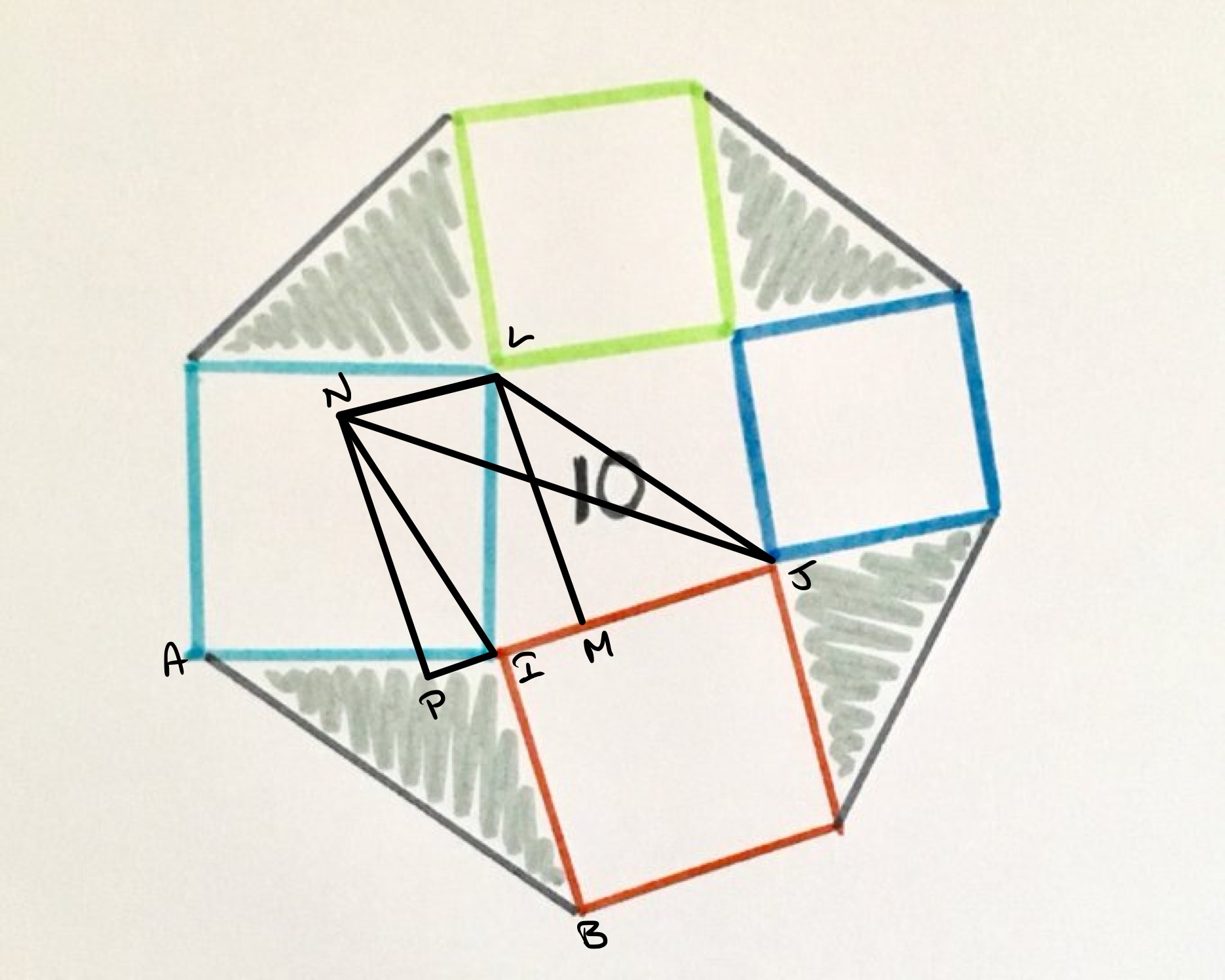
In the above diagram, the point is obtained by shifting parallel to so that has the same length as . This means that triangles and have the same area.
Angles and add up to . This can be seen in various ways, one of which is that reflecting rectangle through the line through takes triangle to .
Angles and also add up to since the angles at a point add up to . Since and have the same length, and and also have the same length, this means that triangles and are congruent and so have the same area.
Putting that together, triangles and have the same area. Following round the same argument for the other grey triangles, each grey triangle has the same area as a triangle formed by cutting the central quadrilateral along a diagonal. So the four grey regions have total area .
Solution by the Sine Rule
This argument follows a similar line to the above, except that showing that triangles and have the same area is deduced from the sine rule. Since angles and add up to , they have the same and so triangles and have the same area.