Notes
four squares and an isosceles triangle solution
Solution to the Four Squares and an Isosceles Triangle Puzzle
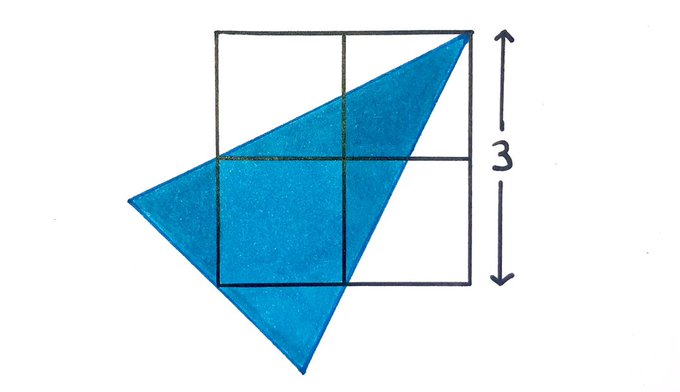
Four squares and an isosceles triangle. What’s the blue area?
Solution by Similar Triangles
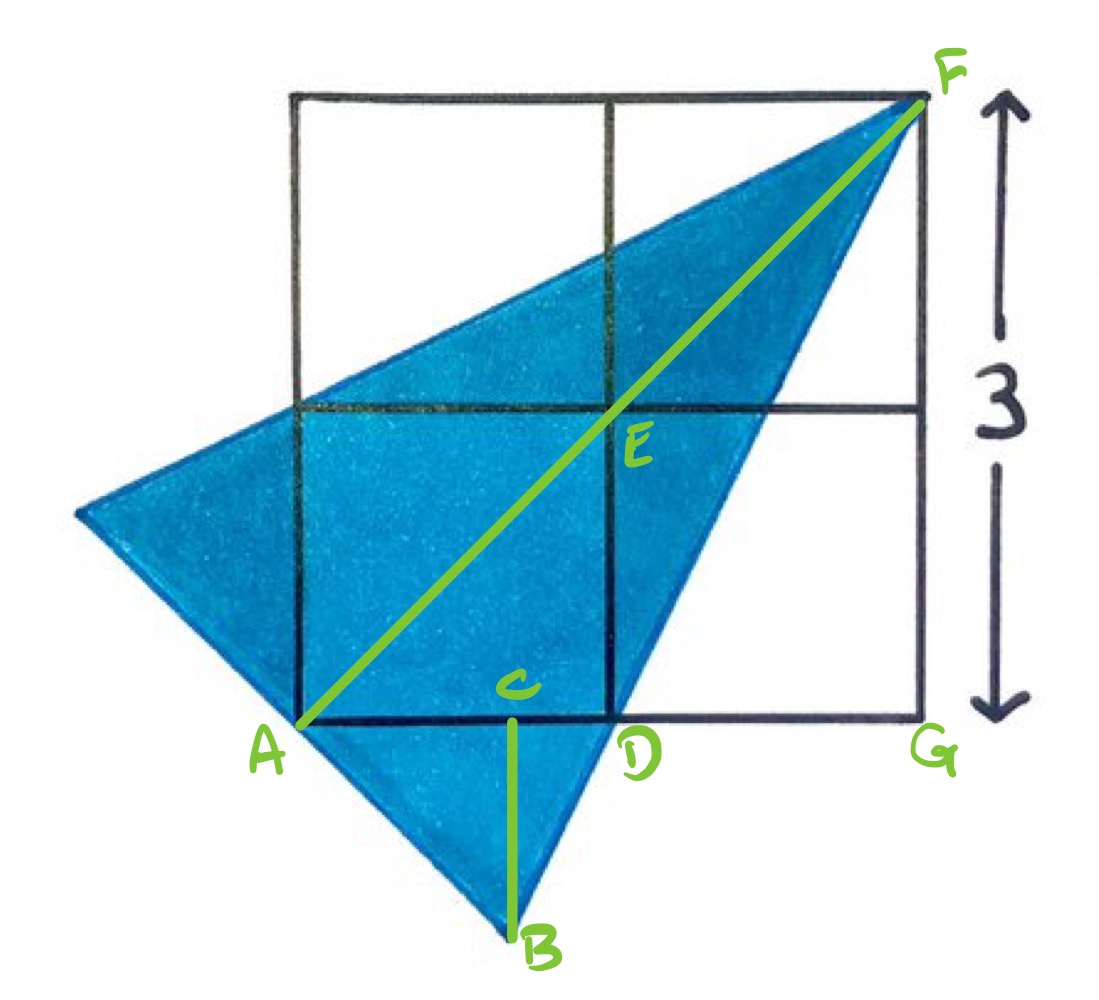
Consider the diagram labelled as above, where point is such that angle is a right-angle.
Angles and are vertically opposite, so triangles and are similar. This means that the lengths of and are in the ratio .
Angle is , so triangle is an isosceles right-angled triangle meaning that and have the same length. This means that the lengths of to are also in the ratio . Since has length , this means that has length , and so also does .
Using the formula for the area of a triangle, triangle has area and has area . So the total area of the blue triangle is: