Notes
four squares and a triangle solution
Solution to the Four Squares and a Triangle Puzzle
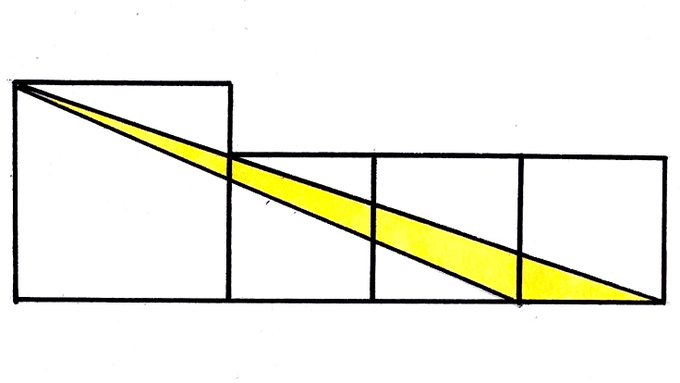
Four squares. What fraction of the total area does the yellow triangle cover?
Solution by Similar Triangles and Area of a Square and Triangle
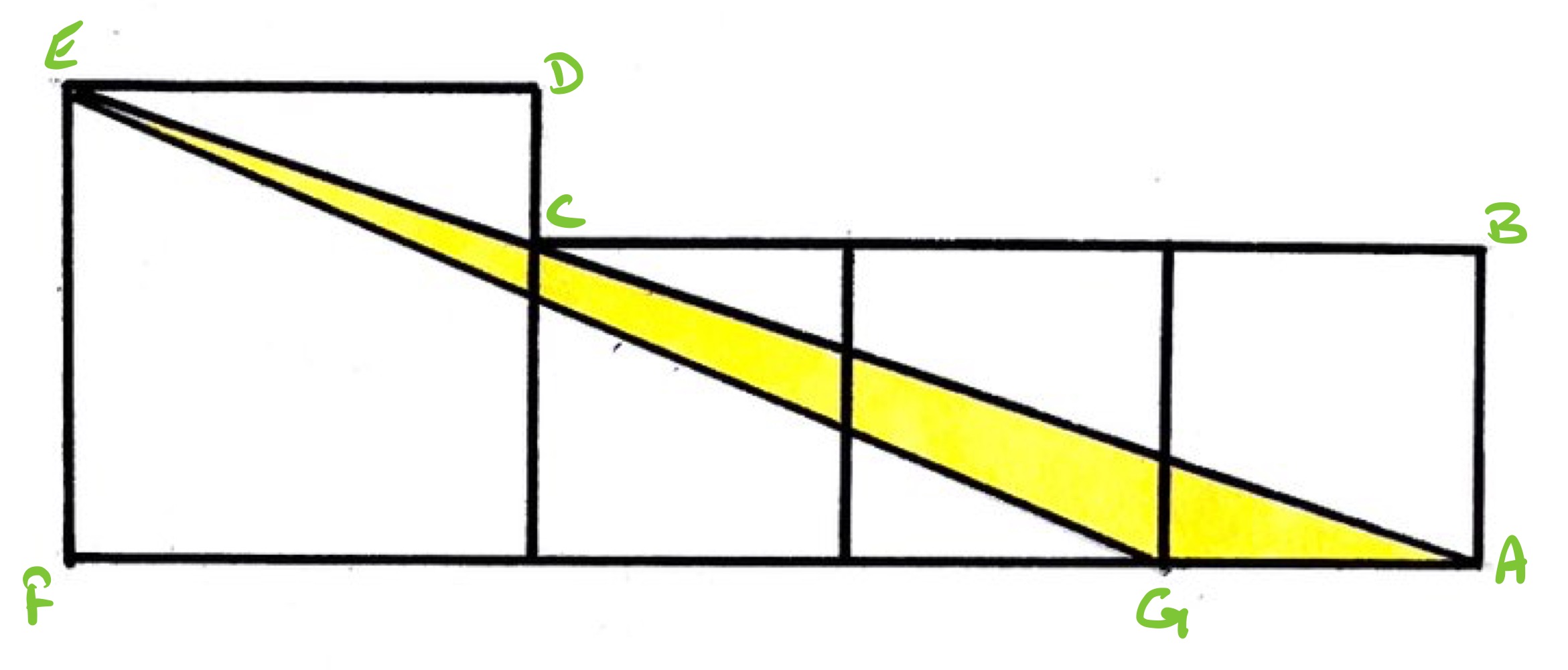
With the points labelled as above, since is a straight line, triangles and are similar. This means that the lengths of and are in the ratio . Since the lengths of and add up to the length of , this means that the lengths of to are in the ratio .
Taking one unit as the length of , so then has length and has length , the area of triangle is . The area of all four squares is .
Therefore the yellow triangle covers th of the total area.