Notes
four squares and a quarter circle solution

Solution to the Four Squares and a Quarter Circle Puzzle

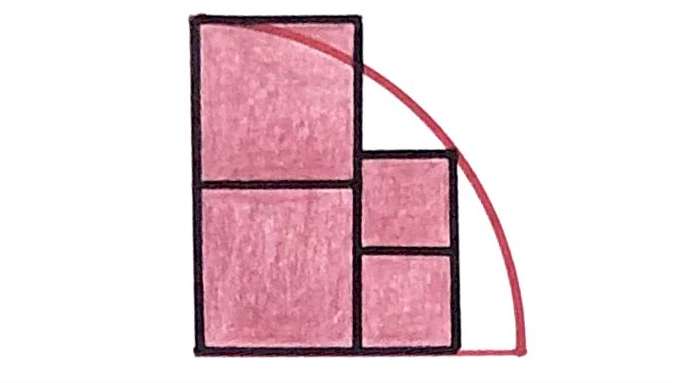
Four Squares and a Quarter Circle

The radius of the quarter circle is $5$ . What’s the total area of the four squares?

Solution by Pythagoras’ Theorem

FourSquaresandaQuarterCircleLabelled.png

Consider the right-angled triangle in the above diagram formed by joining the centre of the circle to the point on the circumference of the circle where the two smaller squares touch it. Let this have height $x$ as in the diagram, then Pythagoras' Theorem says that:

5^2 = x^2 + \left( \frac{5}{2} + \frac{x}{2}\right)^2 = x^2 + \frac{25}{4} + \frac{5}{2} x + \frac{x^2}{4} = \frac{25}{4} + \frac{5}{2} x + \frac{5 x^2}{4}

Rearranging this yields

15 = x^2 + 2x = x(x + 2)

This has solutions $x = 3$ and $x = -5$ , but as $x$ is a length only $x = 3$ is allows.

The area that we are looking for has area:

2 \times \left(\frac{5}{2}\right)^2 + 2 \times \left(\frac{x}{2}\right)^2 = \frac{5^2}{2} + \frac{x^2}{2} = \frac{25}{2} + \frac{9}{2} = 17

Created on May 17, 2021 21:24:55 by Andrew Stacey

Notes four squares and a quarter circle solution

Solution to the Four Squares and a Quarter Circle Puzzle

Solution by Pythagoras’ Theorem

Notes
four squares and a quarter circle solution