Notes
four squares and a quarter circle extension
Extension for the Four Squares and a Quarter Circle Problem
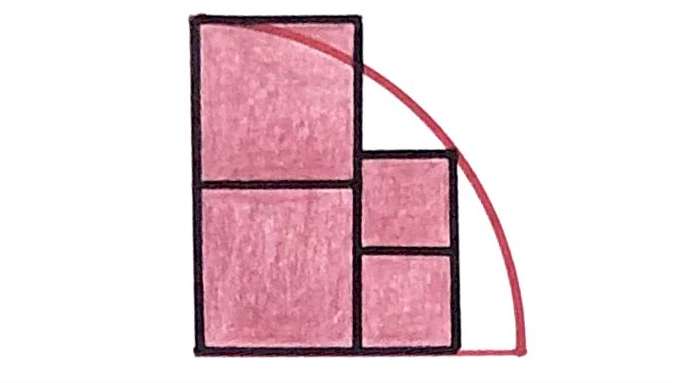
The radius of the quarter circle is . What’s the total area of the four squares?
This problem can be extended as follows. The right way to view the problem for generalising is to see it as two rectangles side by side overlaying a quarter circle. The aspect that will vary is how the rectangles are made up of smaller squares. Pick two positive whole numbers and with (the original problem has and ). The quarter circle will have radius (so in the original it is ). The two rectangles are then made up of squares vertically and squares horizontally. As in the original, the height of the larger rectangle is the radius of the quarter circle, and the smaller rectangle is as large as it can be to fit in the quarter circle.
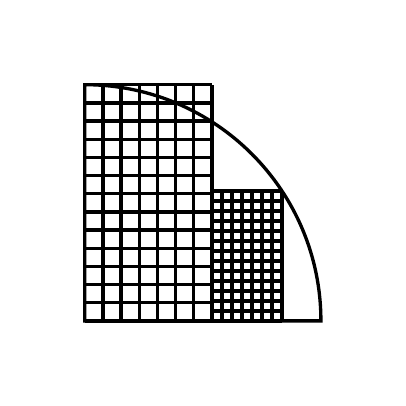
The radius of the quarter circle is . What’s the total area of the squares?
The remarkable part is that the height of the smaller rectangle is a whole number, and the area of the squares is a rational number.
To show this, let us rescale so that the quarter circle has radius and let us write for the width of the larger rectangle and for the height of the smaller one. Then and the smaller rectangle has width . Pythagoras' Theorem says that:
Using the expression for becomes
Scaling up by , the radius of the original quarter circle, then gives a height of the smaller rectangle of . The combined width of the two rectangles is .
We therefore have a Pythagorean triple:
and it turns out that every Pythagorean triple can be obtained in this way.
The areas of the rectangles (in the scaled up version) are then:
In the original problem then meaning that this formula gave a whole number. In general, it will not but it is rational so the whole problem can be scaled up a little more to make it a whole number.
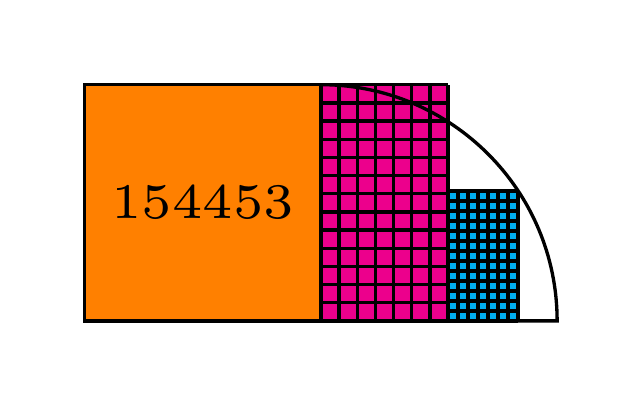
The orange square has area ; the magenta and cyan rectangles are divided into squares with across and up. What is the total area of the magenta and cyan rectangles?