Notes
four quarter circles solution
Solution to the Four Quarter Circles Puzzle
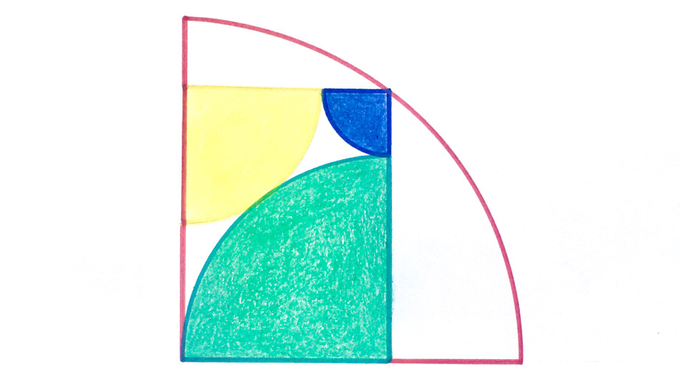
Four quarter circles. What fraction is shaded?
Solution by Area of a Circle and Pythagoras' Theorem
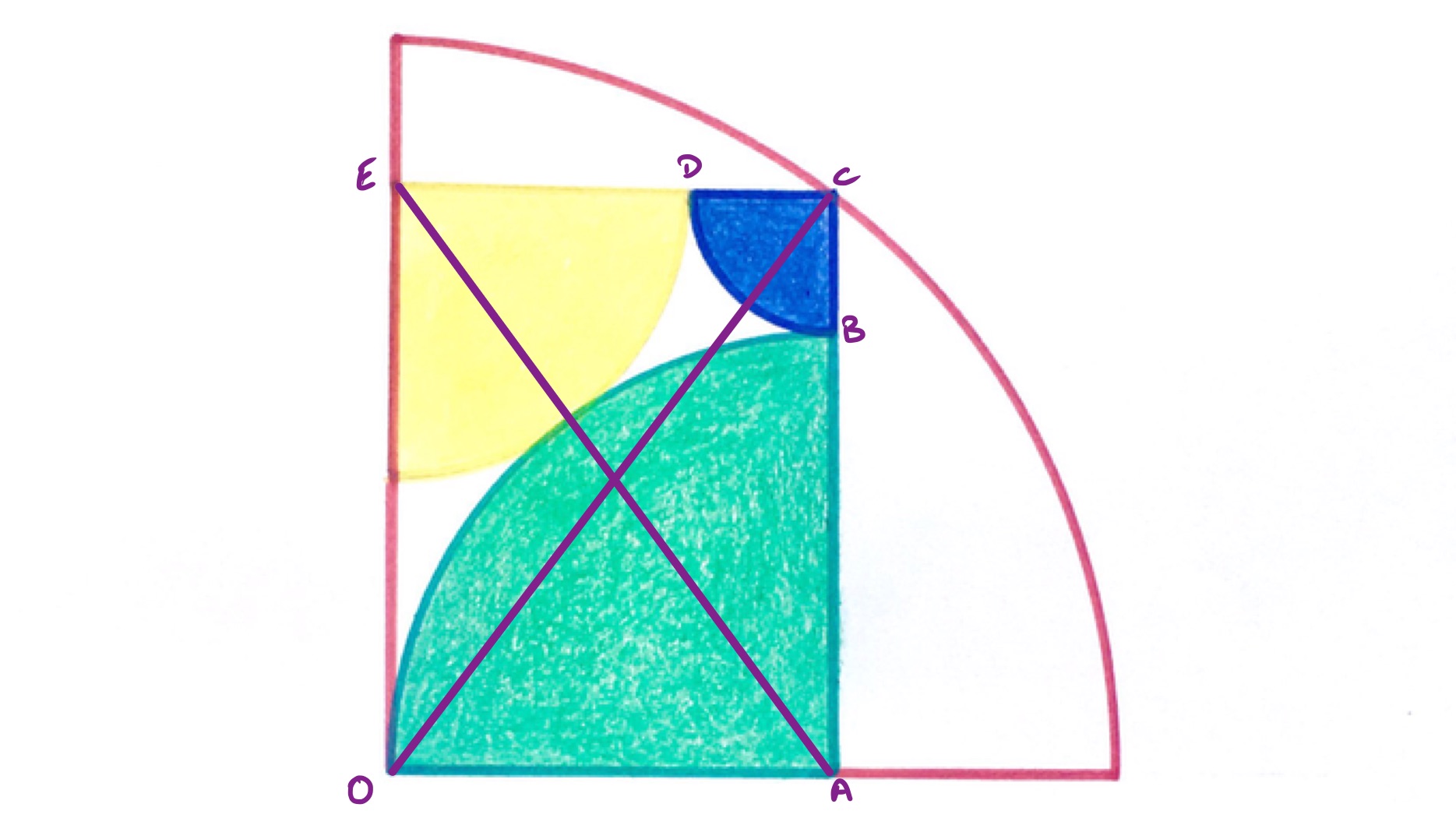
Let , , , be the radii of the quarter circles in increasing length. By considering the width of the rectangle then . The diagonals and have the same length, so .
The equations are slightly simpler with everything expressed in terms of and , so and . Applying Pythagoras' theorem to triangle yields:
But also so and so . Then so , , and .
If using and the resulting equation is which leads to and so, as and are both lengths, then , and .
The area of the outer quarter circle is and the sum of the areas of the shaded quarter circles is . Hence the fraction that is shaded is .