Notes
four quarter circles in a circle solution
Solution to the Four Quarter Circles in a Circle Puzzle
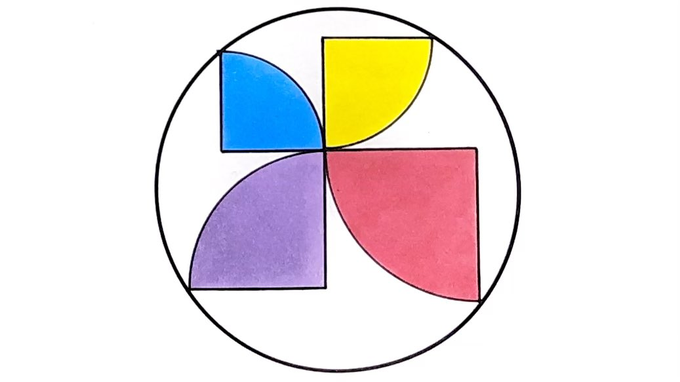
What fraction of the circle do these four quarter circles cover?
Solution by Pythagoras' Theorem
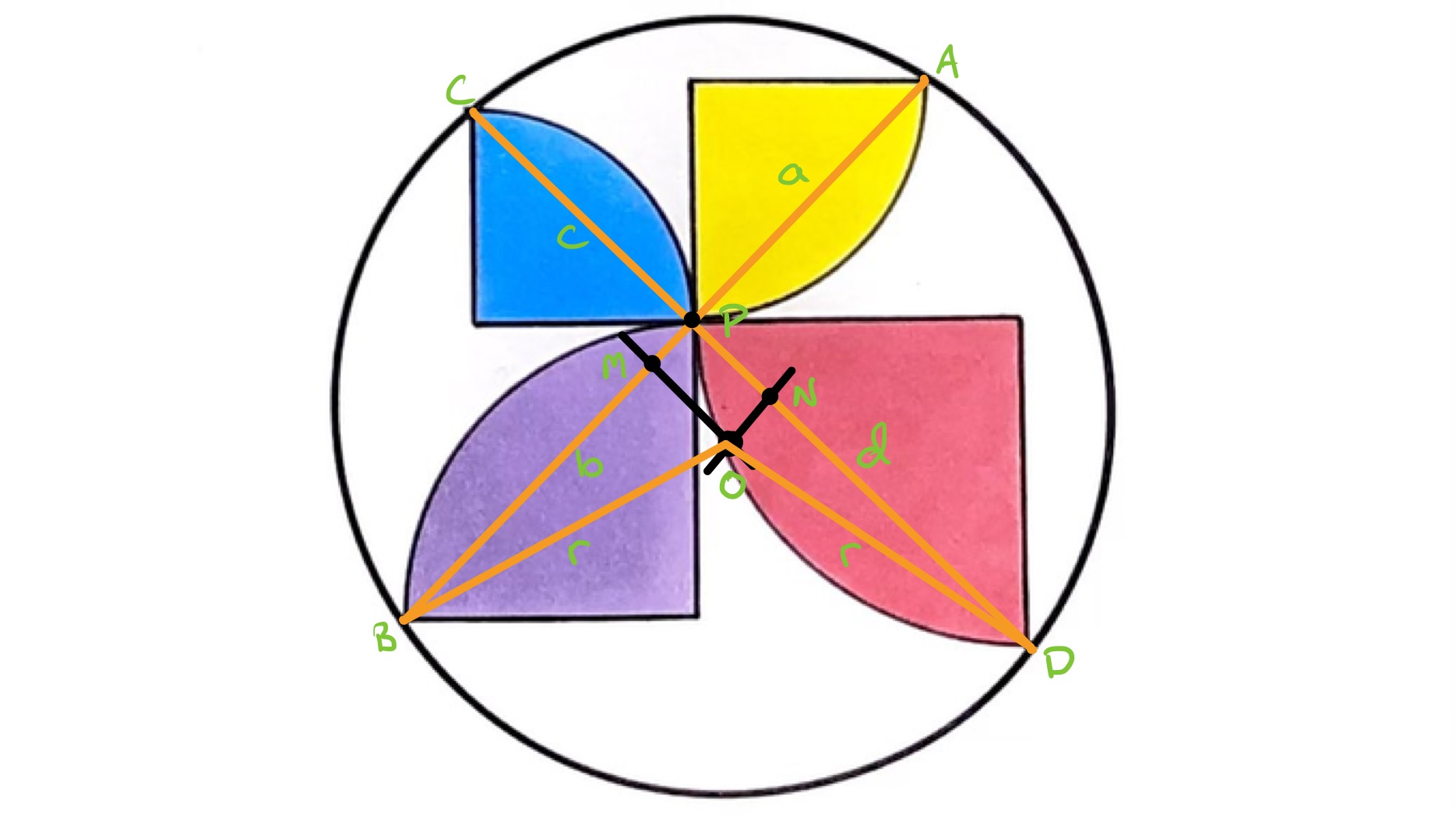
In the above diagram then is the centre of the circle, is the midpoint of , and is the midpoint of . The distances , , , and are measured from the intersection point , and is the radius of the outer circle.
As is the midpoint of , is perpendicular to and similarly is perpendicular to . Since angle is a right-angle, the quadrilateral is a rectangle. In particular, and have the same length as each other, and and have the same length as each other.
Since is the midpoint of , has length and has length . Similarly, has length and has length .
Triangle is a right-angled triangle so applying Pythagoras' theorem results in:
This simplifies to
A similar argument applied to triangle leads to
Taken together, these imply that (this could also be seen through use of the intersecting chords theorem) and so the original equation becomes
The length is the hypotenuse of an isosceles right-angled triangle with radii of the yellow quarter circle forming the other two sides. This radius is therefore of length so the area of that quarter circle is
The total area of the quarter circles is therefore
Since the area of the outer circle is , the shaded area is thus half of the area of the full circle.