Notes
four quarter circles ii solution
Solution to the Four Quarter Circles II Puzzle
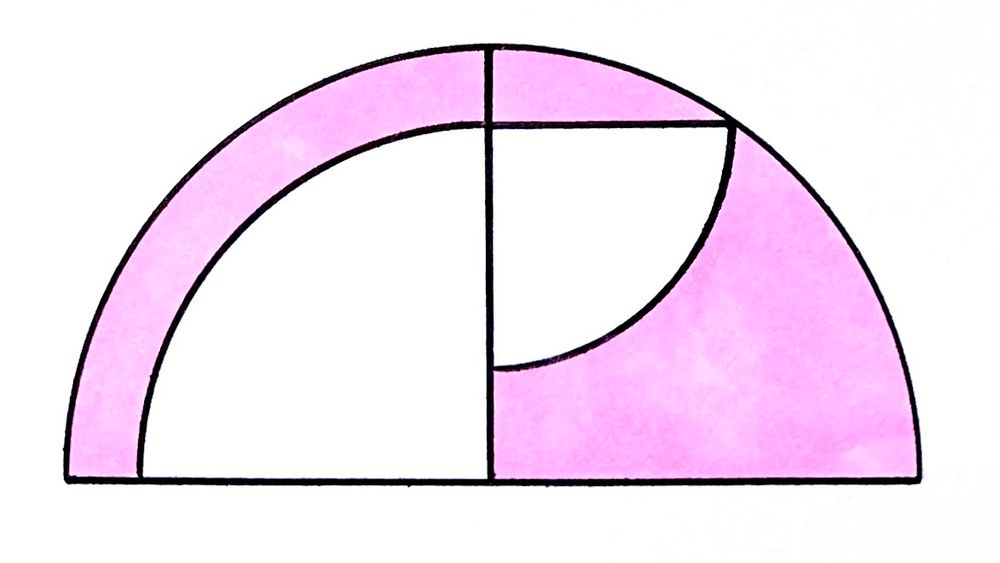
Four quarter circles. What fraction is shaded?
Solution by Pythagoras' Theorem and Area of a Circle
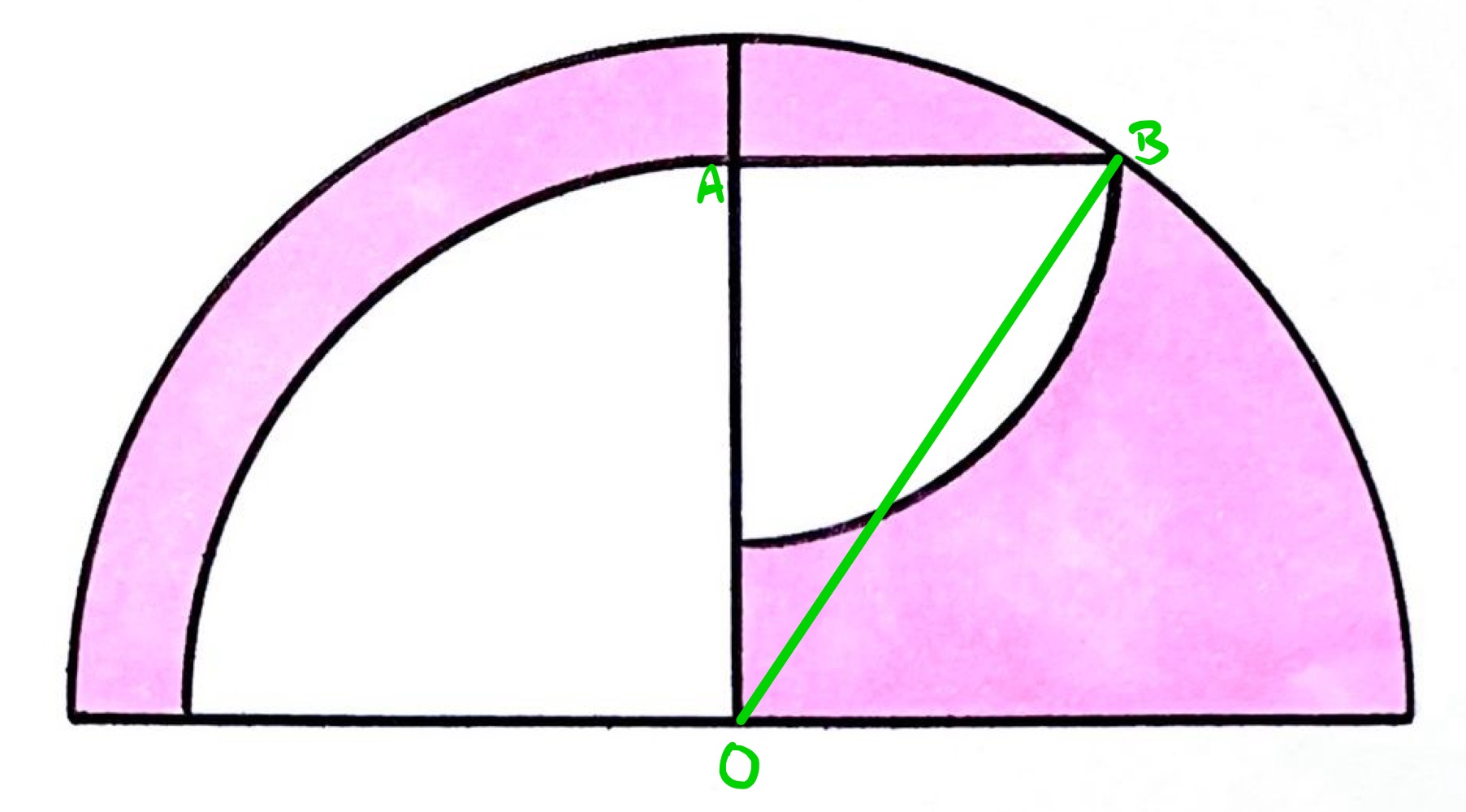
With the points labelled as above, is the centre of the semi-circle and left-hand quarter circle, while is the centre of the right-hand quarter circle. Let , , and be the lengths of their respective radii, so has length , has length , and has length .
Using the formula for the area of a circle, the area of the shaded region is:
(1)
Triangle is right-angled so Pythagoras' theorem applies, meaning that . Substituting into Equation (1) shows that the shaded region has area:
and this is half of the area of the full semi-circle.
Solution by Invariance Principle
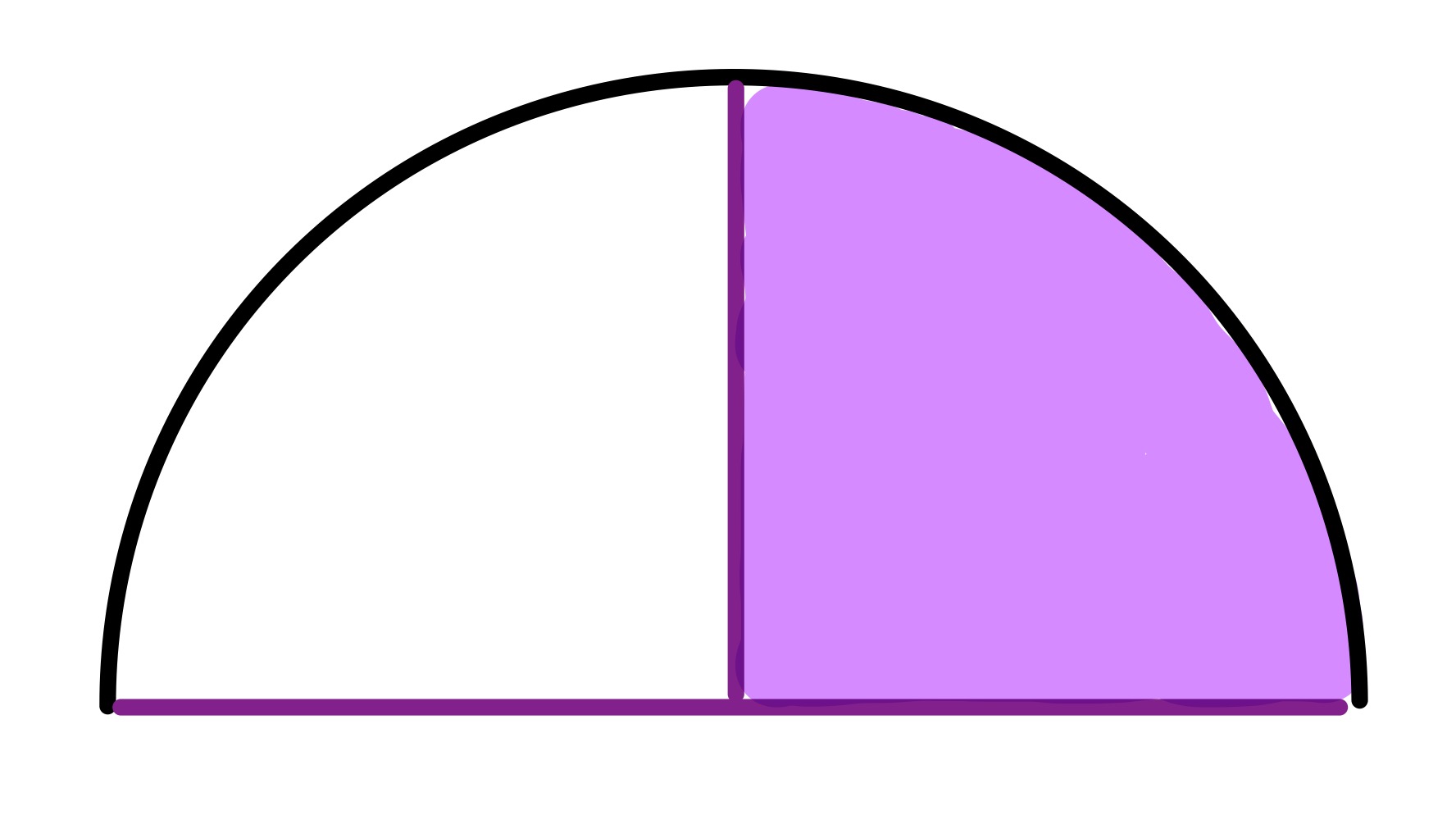
The inner quarter circles can be varied, and the configuration above shows that the shaded region comprises half of the overall diagram.