Notes
four parallel semi-circles solution

Solution to the Four Parallel Semi-Circles Puzzle

Solution by Properties of Chords and Pythagoras' Theorem

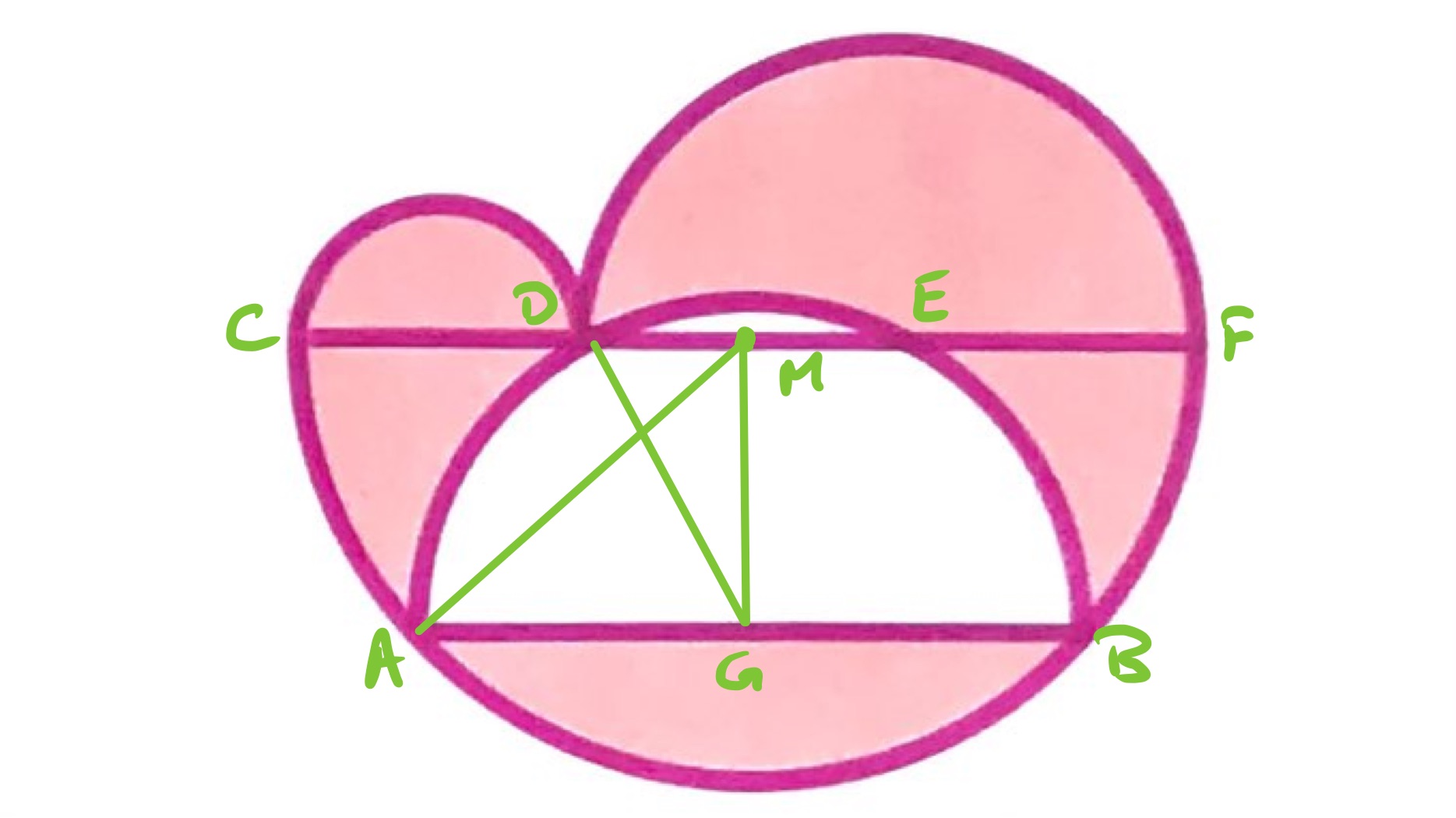
In the above diagram, the points labelled $G$ and $M$ are the centres of their semi-circles. Since $A B$ is a chord on the largest semi-circle, and $G$ is its midpoint, the line $G M$ is perpendicular to $A B$ and so also perpendicular to $C F$. Triangles $G M D$ and $M G A$ are therefore a right-angled triangles.

Let $a$, $b$, and $c$ be the radii of the semi-circles other than the largest, with the length of $C D$ as $2a$, of $D F$ as $2 b$, and of $A B$ as $2 c$. Since $C F$ has length $8$, $2 a + 2 b = 8$ so $a + b = 4$. As $M$ is the midpoint of $C F$, $C M$ has length $a + b$, so $D M$ has length $b - a$. Let $d$ be the length of $G M$.

Applying Pythagoras' theorem to triangles $G M D$ and $M G A$ shows that:

Putting these together and eliminating $d^2$ shows that:

Since $a + b = 4$, $4^2 = (a + b)^2 = a^2 + 2 a b + b^2$, so $2 a b = 16 - a^2 - b^2$. Substituting this in shows that:

So $c^2 = a^2 + b^2$.

From the area of a circle, the shaded area is given by:

Solution by Agg Invariance Principle

The point labelled $D$ in the above diagram can move along the diameter $C F$.

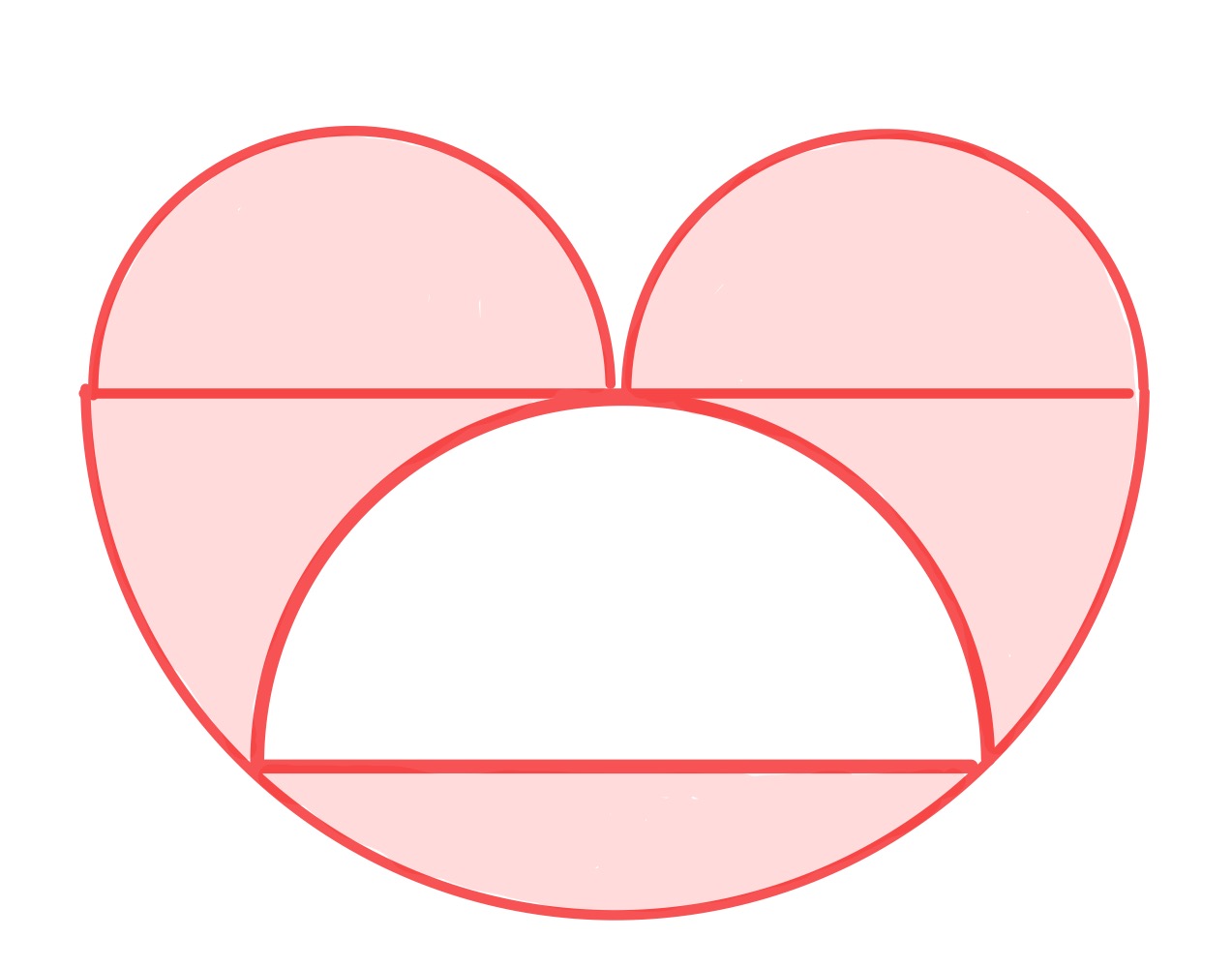
With $D$ at the midpoint the radii of the circles are in the ratio $1:\sqrt{2}:2$ so their areas are in the ratio $1 : 2 : 4$. The two smaller semi-circles therefore have the same area as the middle one, leaving the equivalent of the largest semi-circle in total area.

Placing $D$ at the end of the diameter, the white semi-circle coincides with one of the upper semi-circles, and the other has zero size. The shaded area is therefore just the lower semi-circle.