Notes
four isosceles triangles in a circle solution
Four Isosceles Triangles in a Circle
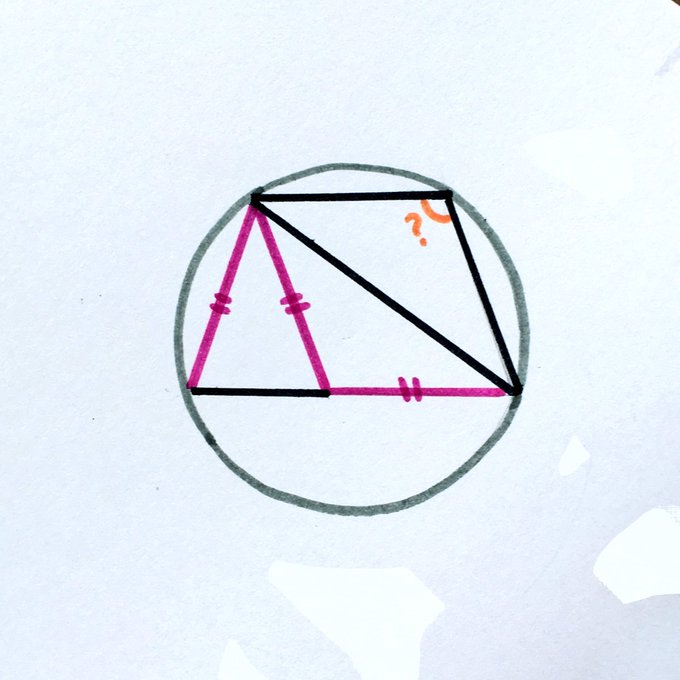
All four triangles are isosceles. What’s the angle?
Solution by Isosceles Triangles and Cyclic Quadrilateral
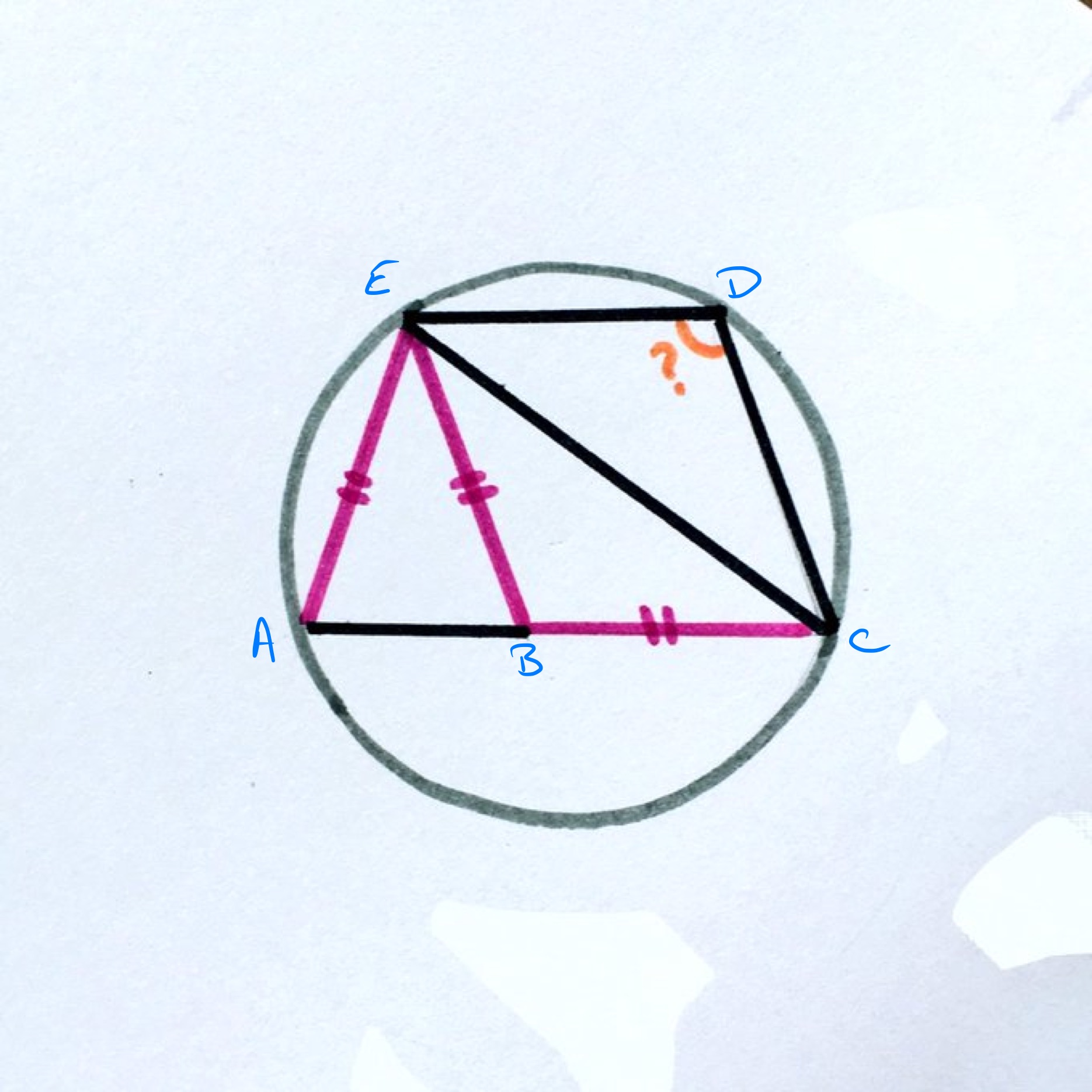
Let be angle . As triangle is isosceles, angle is . As triangle is also isosceles, angle is also and angle is also . Since triangle is isosceles, angle is also . Looking at angle , then which means that . Lastly, the quadrilateral is cyclic so angle is .