Notes
four houses in a semi-circle solution
Solution to the Four Houses in a Semi-Circle Puzzle
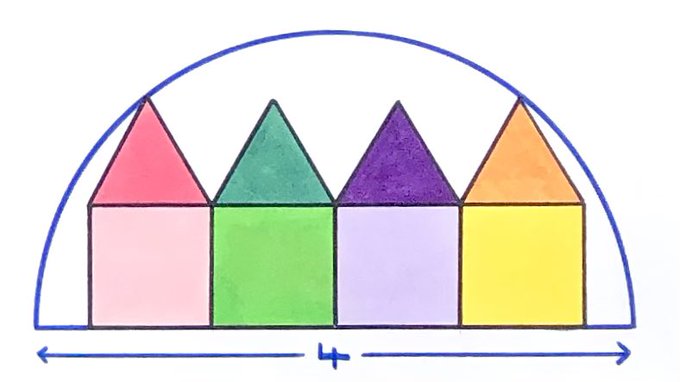
These houses are made from squares and equilateral triangles. What’s their total area?
Solution by Properties of an Equilateral Triangle and Pythagoras' Theorem
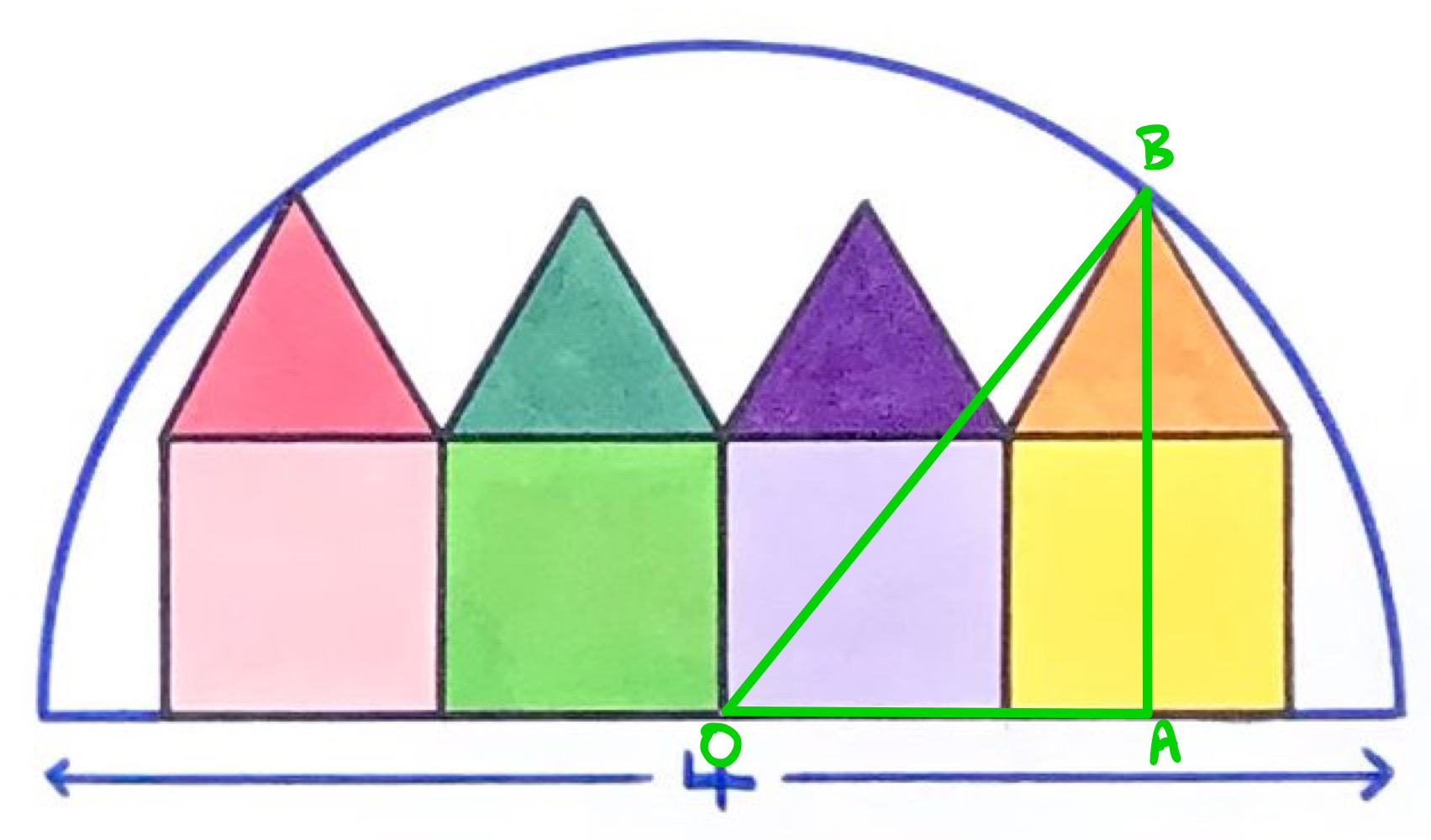
As the squares and equilateral triangles all share edges, all those edges are the same length. Let this length be .
In the diagram above, is the centre of the circle and is such that angle is a right-angle. Since is the apex of an equilateral triangle, bisects the base of that triangle, and hence also of the square below it.
Line segment is a radius of the circle so has length . Line segment comprises one-and-a-half of the sides of the squares, so has length . Then line segment is the height of one square and the height of one equilateral triangle, so from the lengths in an equilateral triangle is has length .
Applying Pythagoras' theorem to triangle then:
From the properties of an equilateral triangle, the area of one with side length is . So the total area of the squares and triangles is .