Notes
four equilateral triangles solution
Solution to the Four Equilateral Triangles Puzzle
Posted on Aug 13, 2018
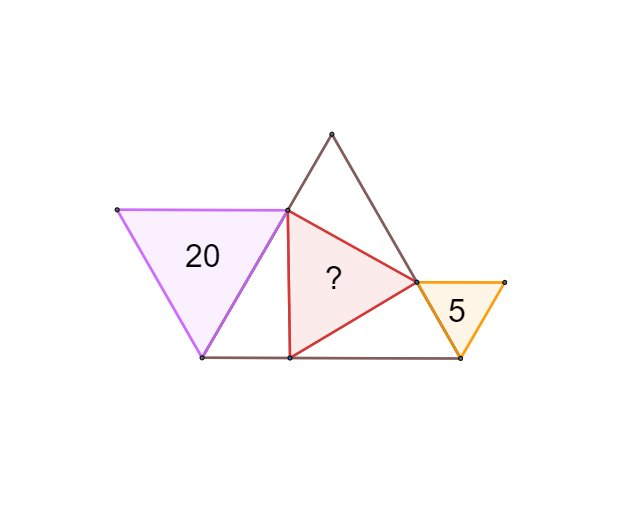
Here are equilateral triangles. Find the missing area.
Solution by Properties of Equilateral Triangles
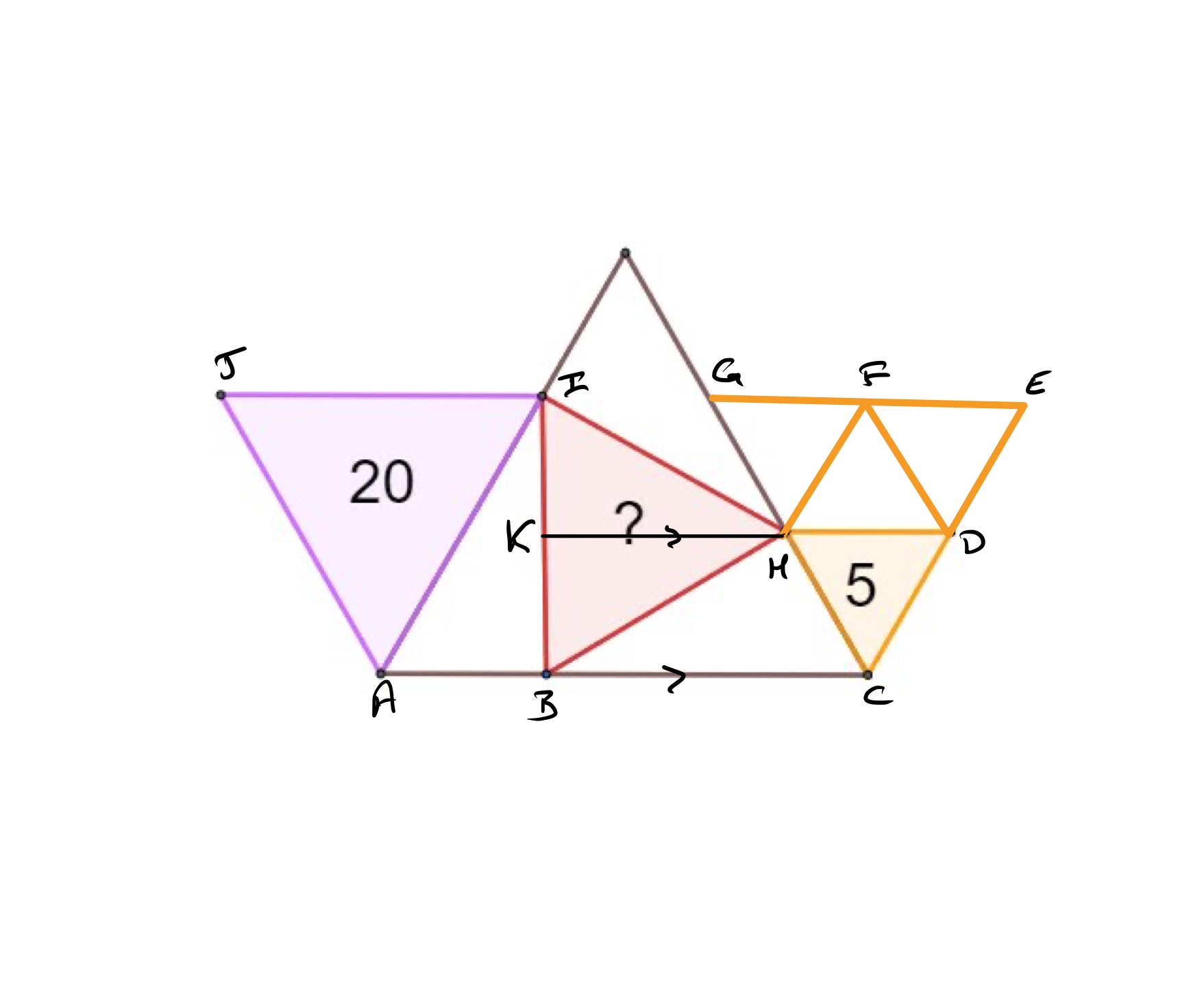
With the points labelled as above, the equilateral triangle is formed by taking four copies of and assembling them into a single triangle. Its area is therefore , so it is congruent to triangle . Since and have the same length, this means that the height of above is half the height of .
The point is so that is parallel to . Since the height of above is half that of , is also the midpoint of . As triangle is equilateral, angle is a right-angle and so is perpendicular to . The length of is thus the height of the triangle . From lengths in an equilateral triangle, the length of is times the length of , so the area of is that of triangle , namely .
Solution by Dissection and Symmetry
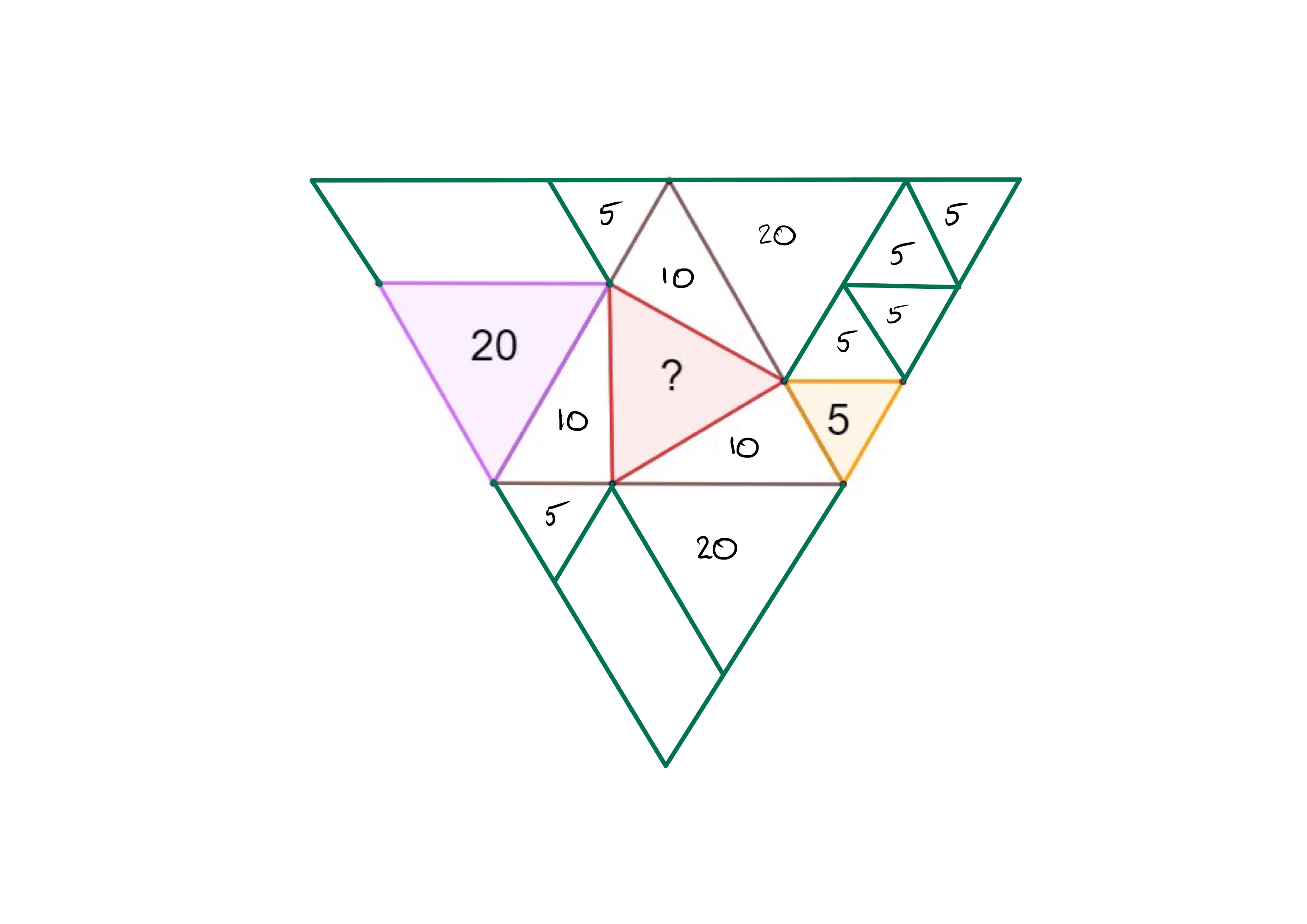
In the above diagram, the original diagram has been extended so that the outer shape is an equilateral triangle. The outer triangle consists of four copies of the middle triangle of the original diagram. Looking at the upper right triangle, the area of one of these four is .
In the central triangle, the three right-angled triangles are all half of the pink triangle, so have area . This leaves for the red triangle.