Notes
four equilateral triangles round a square solution
Four Equilateral Triangles Round a Square
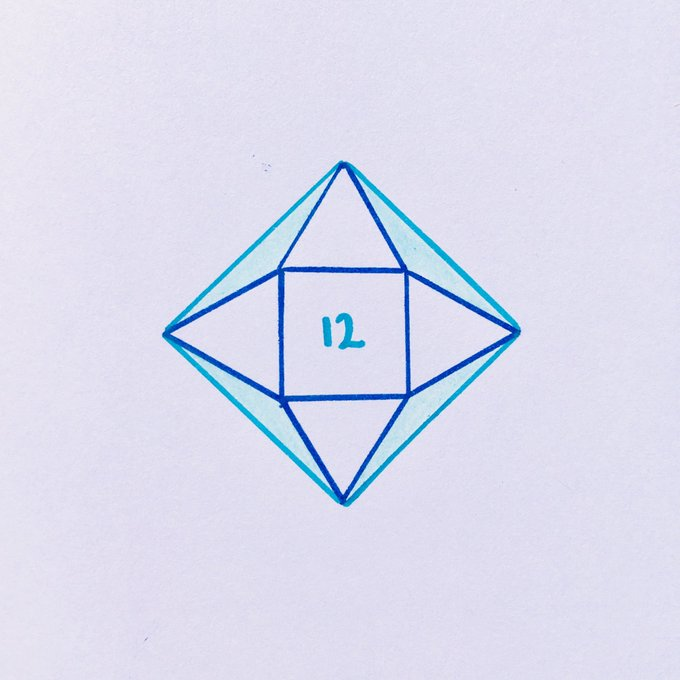
Four equilateral triangles are arranged around a square which has area . What’s the total shaded area?
Solution by Properties of an Equilateral Triangle
Let be the side length of the inner square, so that . From the relationships between the lengths in an equilateral triangle, the height of the equilateral triangles is and so the diagonal of the outer square is . The area of the outer square is therefore:
The area of each equilateral triangle is and so the area of all four is . Hence the shaded area is .