Notes
four equilateral triangles inside a hexagon solution
Solution to the four equilateral triangles inside a hexagon Puzzle
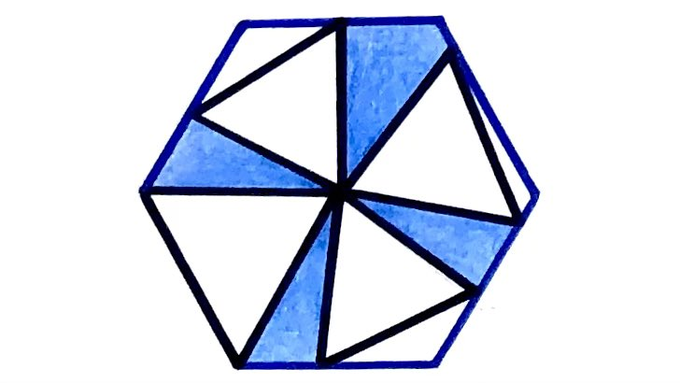
Four equilateral triangles inside a regular hexagon. What fraction is shaded?
Solution by Symmetry
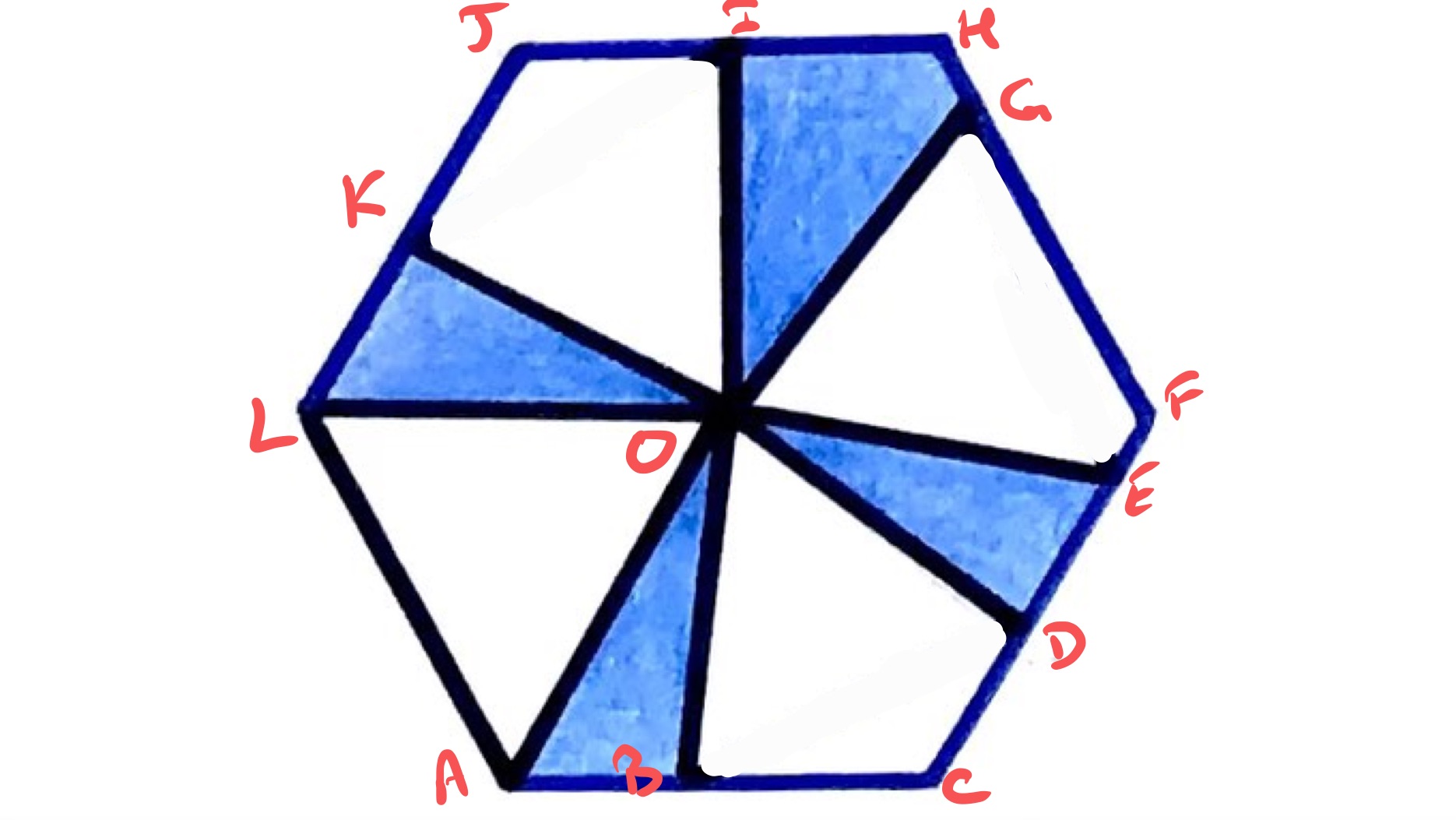
The solution to this is perhaps easier to see if some of the lines are removed, as in the above diagram. The angles at the centre of the white regions are all . As the hexagon is invariant under rotating by , this means that when rotating anticlockwise by then maps to , to , and to .
Therefore, rotating triangle by clockwise brings along , creating a new region . Rotating this region by clockwise brings , creating a new region . Lastly, rotating this region by brings to with the final region .
This is of the area of the hexagon.