Notes
four congruent triangles solution
Solution to the Four Congruent Triangles Puzzle
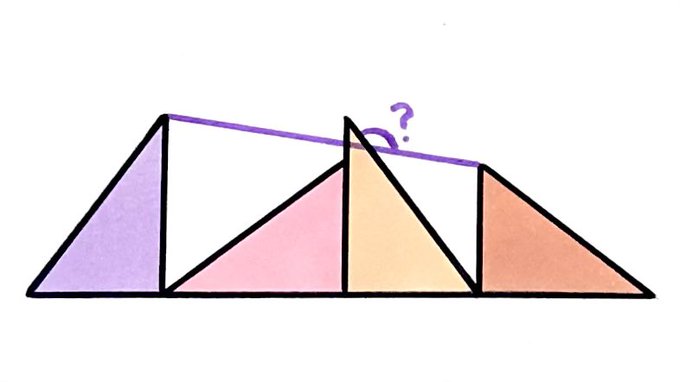
These four congruent triangles are laid out along a straight line. What’s the angle?
Solution by Angles in an Isosceles Right-Angled Triangle and Congruent Triangles
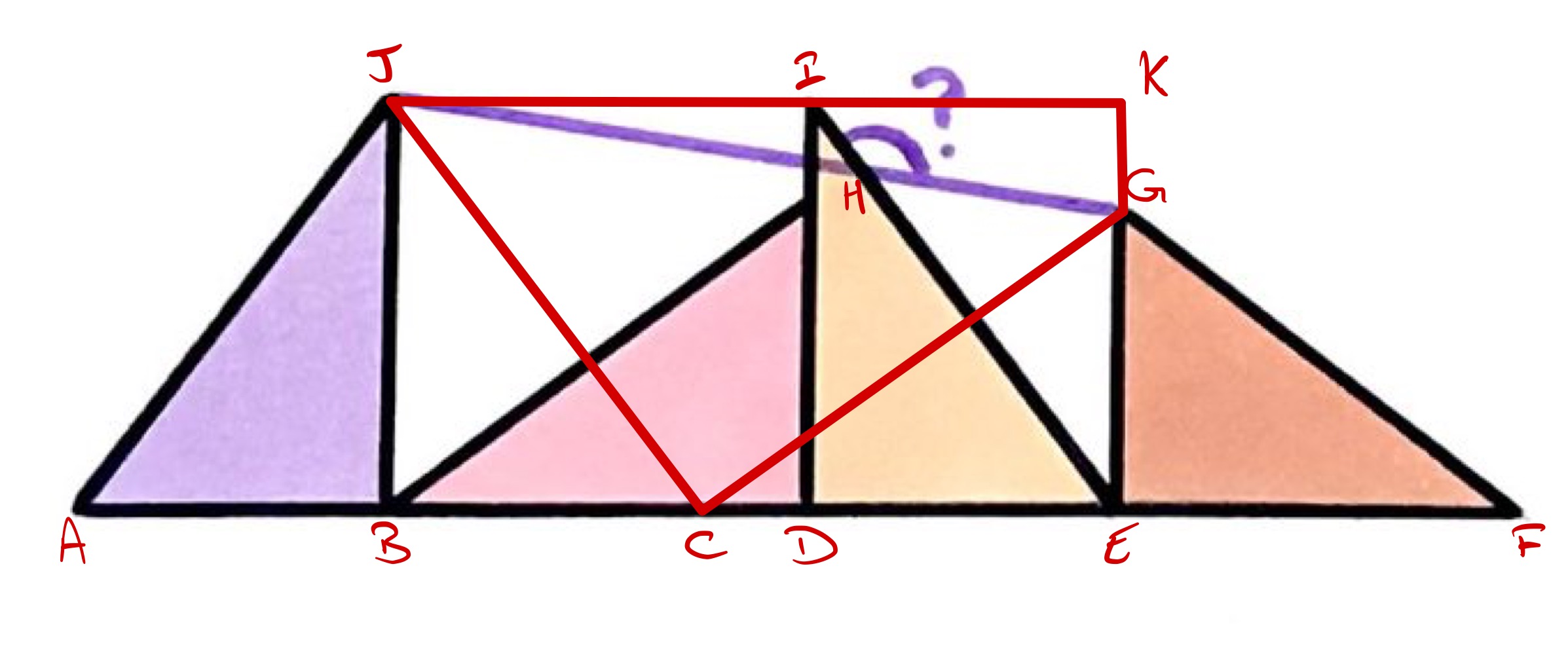
Label the diagram as above, in which is the point on such that line segment has the same length as .
In effect, the diagram with triangles , , , and is obtained from the original by swapping the positions of the two middle triangles. So triangles and are also congruent to the original four.
Since is a straight line, and angles and are equal, they must be . So the triangles are all right-angled. This means that angles and add up to , since angles in a triangle add up to , and so angle is , since angles at a point on a straight line add up to .
Then as and are corresponding sides of congruent triangles, they have the same length, so triangle is an isosceles right-angled triangle. Angle is therefore .
Then as and are parallel, angle is also , since corresponding angles are equal. Hence angle is .
Solution by the Compound Angle Formulae in Trigonometry
With the points labelled as above, in which is such that is parallel to and is a straight line, let the sides of the main triangle be and , with . Let denote angle . Then .
Consider triangle . Its side lengths are and . Let denote angle , then:
Since both are acute, this means that . Therefore, angle and so angle .