Notes
four congruent squares inside a larger square solution
Solution to the Four Congruent Squares Inside a Larger Square Puzzle
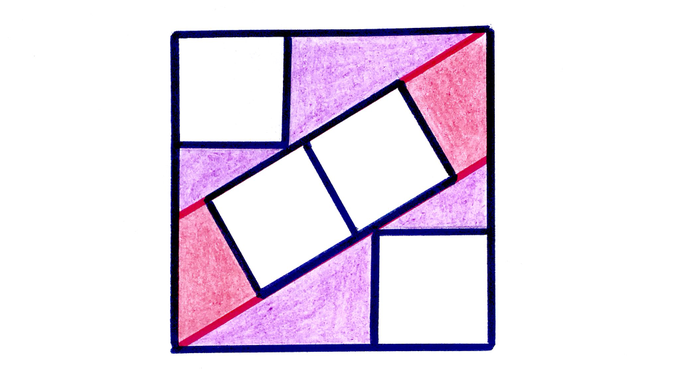
Four of the five squares are congruent. What’s the ratio of red to purple?
Solution by Similar Triangles and Pythagoras' Theorem
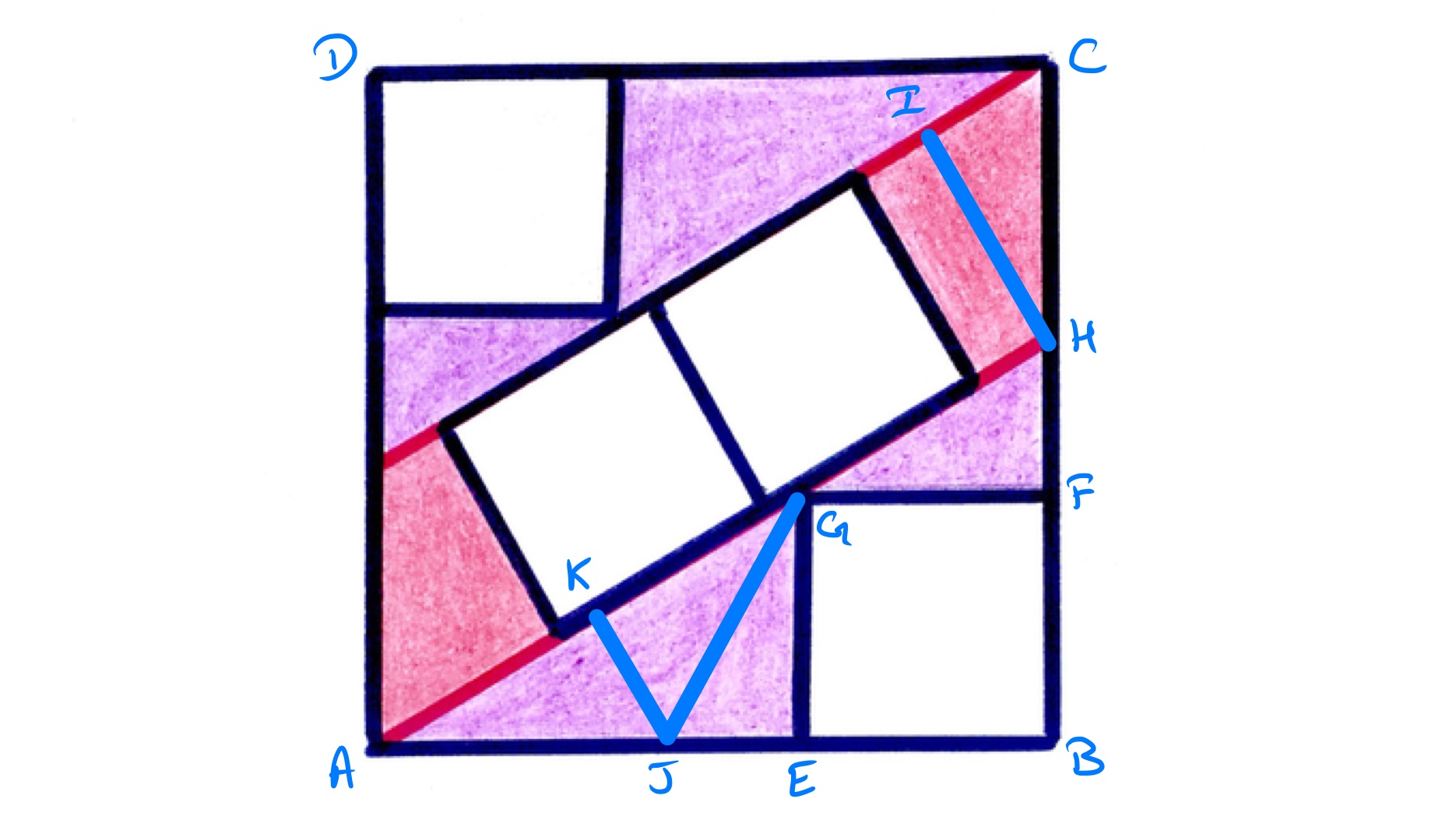
With the points labelled as above, let , , be the side lengths of the right-angled triangle in increasing order, so that is the length of , of , and of . Pythagoras' theorem gives the relationship .
Triangle is congruent to triangle since angle is equal to angle and the lengths of and are equal. So has length and thus the side length of the outer square is .
This means that has length . Triangle is similar to triangle , so the ratios and are equal. This gives the relationship . Putting this in to the equation above from Pythagoras’ theorem yields , or . This has solutions or . Since and are lengths (and so positive), it must be that .
The total area of purple regions is then .
To find the red area, note that triangle is similar to triangle and so the length of is double that of , which is . So the length of is . The sum of the two red segments is therefore . The red regions can therefore be put together to form a rectangle with side lengths and , so the area of the red regions is .
Therefore the ratio of red to purple is .
Solution by Similar Triangles and Hidden Point
This solution is similar to the above, except that it uses properties of similar triangles instead of Pythagoras' theorem and so avoids factorising a quadratic. Having noted, as above, that the length of is , let be the point on so that has length and length . Then , , and are all congruent triangles, and so the length of is twice that of . The rest of the proof continues as above.