Notes
five triangles in a rectangle solution

Five Triangles in a Rectangle

Solution by Pythagoras' Theorem

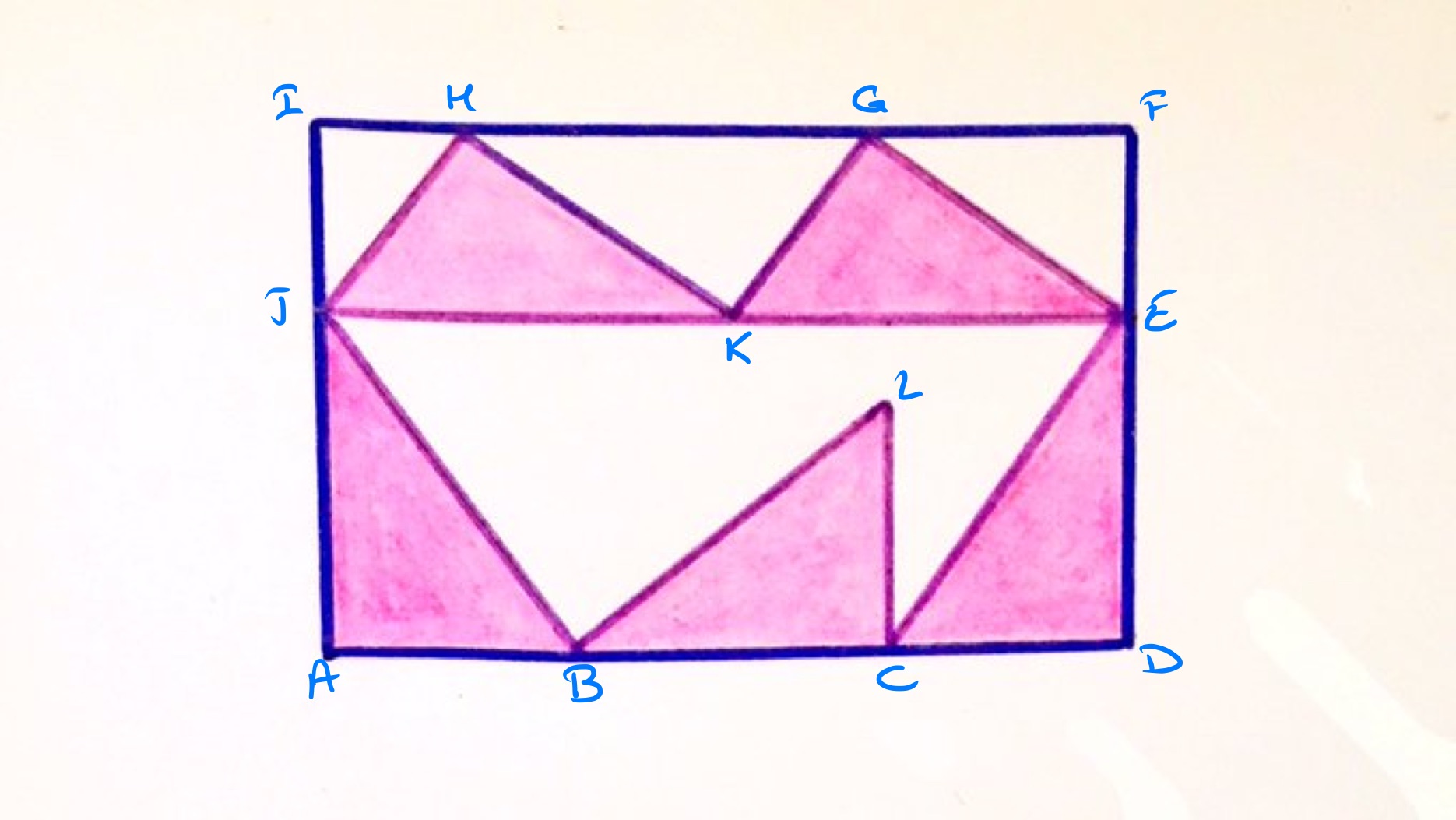
With the points labelled as above, let $a$, $b$, and $c$ be the lengths of the sides of the triangle in increasing order, so that $a$ is the length of $A B$, $b$ of $A J$, and $c$ of $B J$. Comparing the lengths of $E J$ with $A D$ gives the identity $2 c = 2 a + b$. Since triangle $B A J$ fits in the corner of the rectangle, it is a right-angled triangle and so Pythagoras' theorem applies to give that $c^2 = a^2 + b^2$.

Squaring the first identity shows that $4 c^2 = 4 a^2 + 4 a b + b^2$ which shows that $3 b^2 = 4 a b$ and so $4 a = 3 b$. Let $x = \frac{1}{3} a$, then $a = 3x$, $b = 4x$, and $c = 5x$.

The area of one triangle is then $\frac{1}{2} \times 3 x \times 4 x = 6 x^2$, so the area of all the triangles is $30 x^2$. To calculate the area of the rectangle, split it along $J E$. The area of $J E F I$ is the area of four triangles, so is $24 x^2$. The area of $A D E J$ is $b \times 2 c = 4 x \times 10 x = 40 x^2$. The total area is then $64 x^2$. The fraction of the rectangle covered is therefore $\frac{40}{64} = \frac{5}{8}$.