Notes
five squares solution
Solution to the Five Squares Puzzle
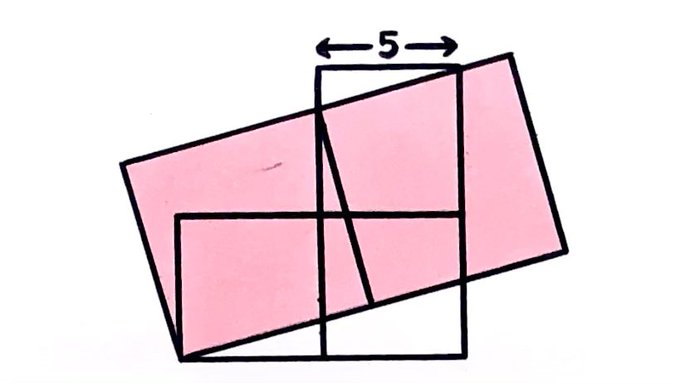
Five squares. What’s the total shaded area?
Solution by Similar Triangles
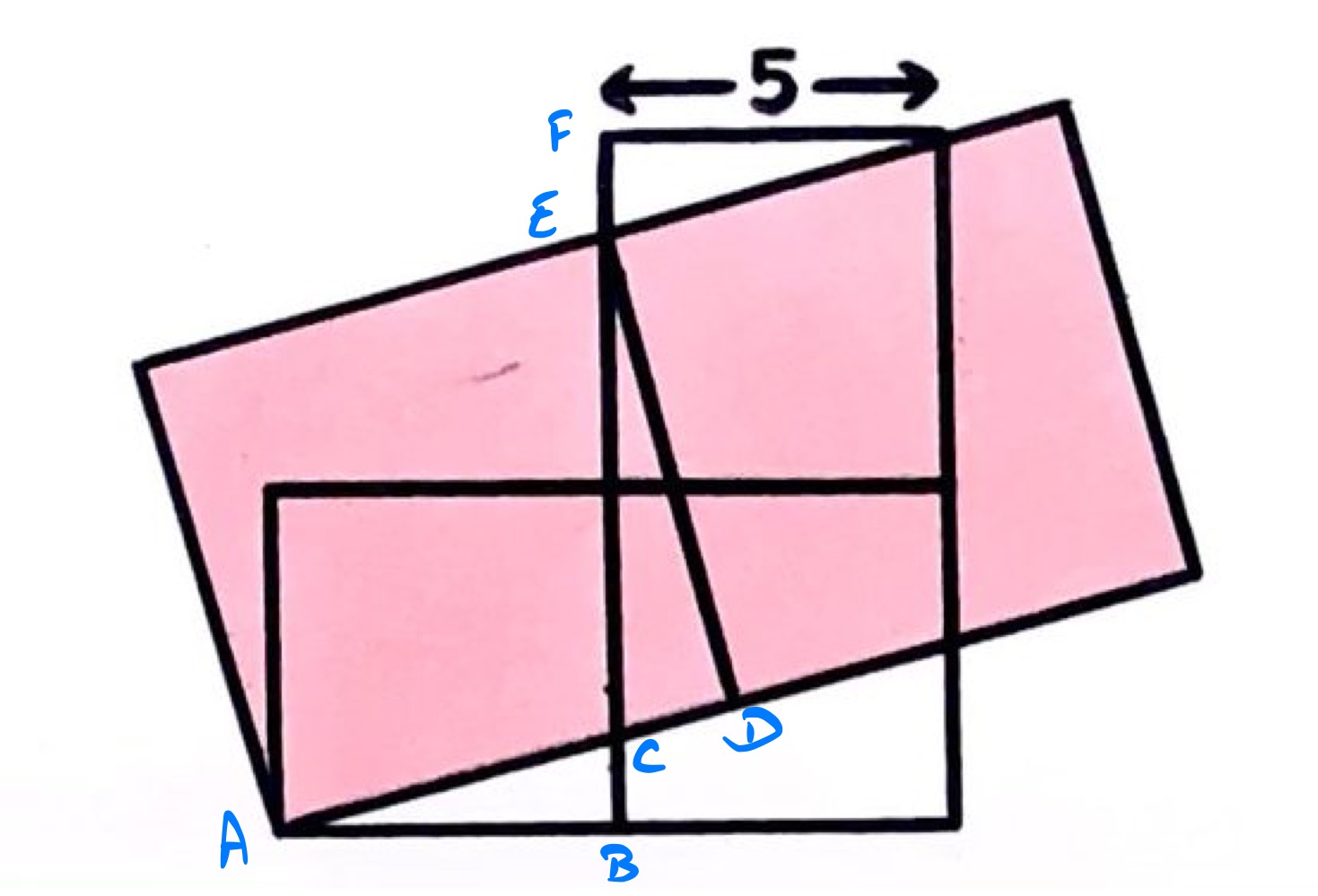
With the points labelled as above, angles and are the same since they are vertically opposite. Then as triangles and are right-angled and have an angle in common, they are similar.
Let , , and be the lengths of line segments , , and respectively. Then the lengths of line segments , , and , are, respectively, , , and . So by similarity:
The second of these rearranges as follows:
Then using the first:
So . Since is the side length of the tilted squares, the total shaded area is .
These rearrange to and .