Notes
five squares across a square solution
Solution to the Five Squares Across a Square Puzzle
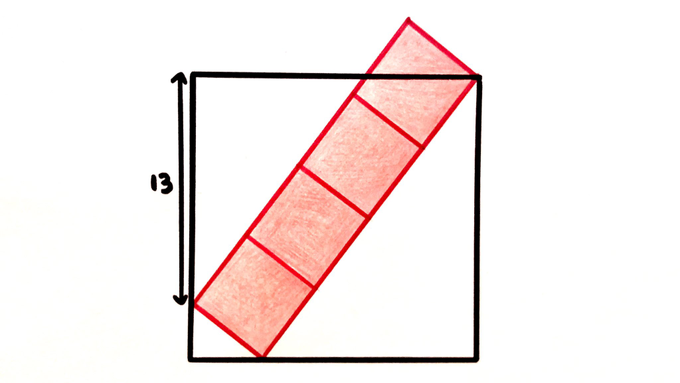
Five squares. What’s the total shaded area?
Solution by Similar Triangles
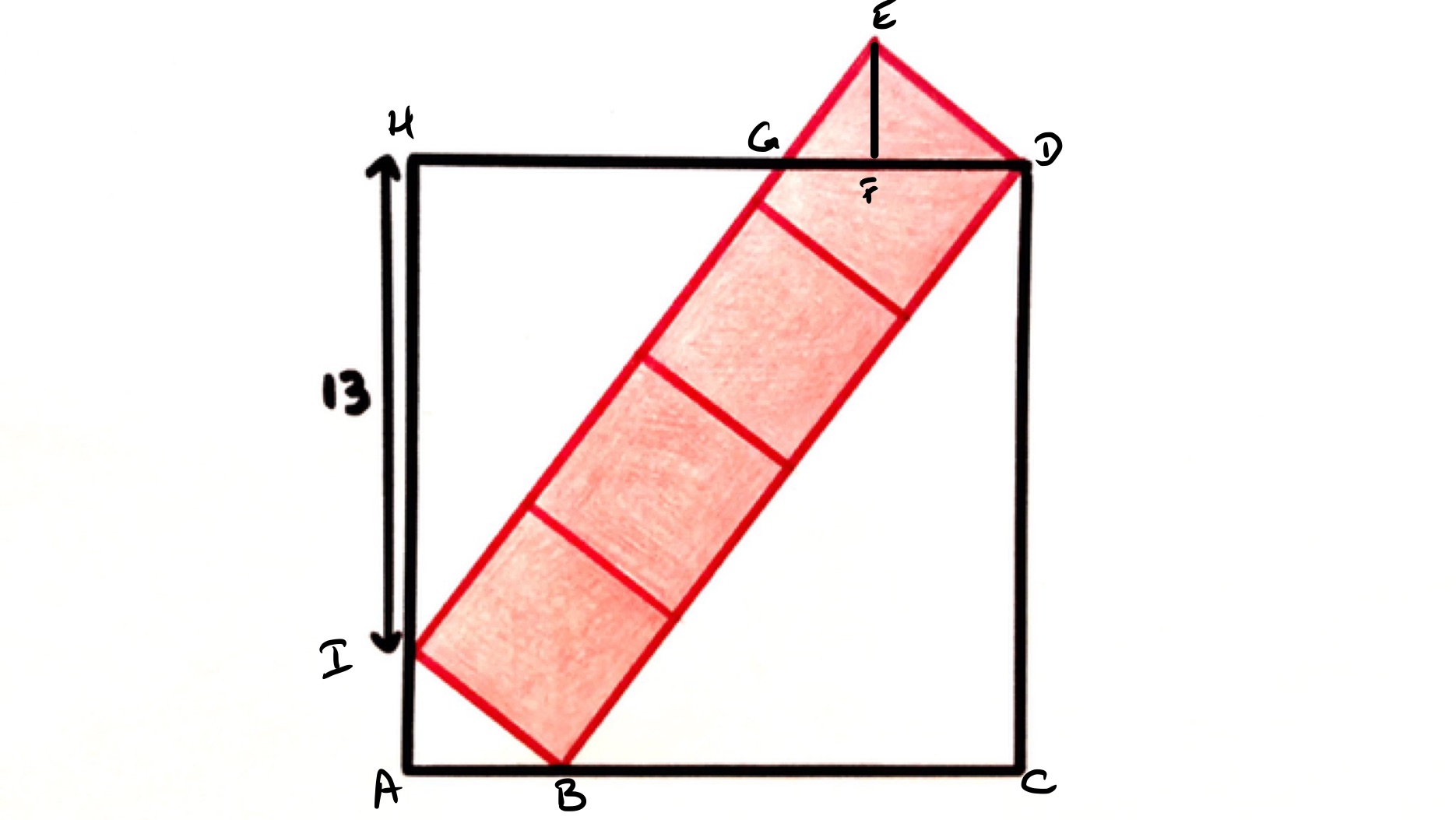
There are many similar triangles in this diagram (using angles on a straight line and angles in a triangle to demonstrate their similarity). Triangles , , and are all similar (with vertices corresponding in the given orders). The length of is four times that of , so the lengths of and are four times those of and respectively. Since and have the same length, must therefore be of the length of . Then the length of is of that of , which is a quarter of the length of , so the length of is of the length of . The remainder of the side , namely , is therefore of the full length. As this side has length , the side length of the square is therefore .
Many of the lengths can now be filled in:
- has length
- has length
- has length
- has length
- has length
- has the same length as , namely ( is the point directly below on )
The side length of the shaded squares can be calculated as using Pythagoras' Theorem giving a total shaded area as , but that is not necessary to solve the stated problem as the shaded area can be calculated by finding the areas of the white triangles using the lengths above, subtracting that from the area of the square, and adding the area of triangle . These areas are:
- has area
- has area
- has area
- has area
- has area
So the shaded region has area: