Notes
five semi-circles solution
Solution to the Five Semi-Circles Puzzle
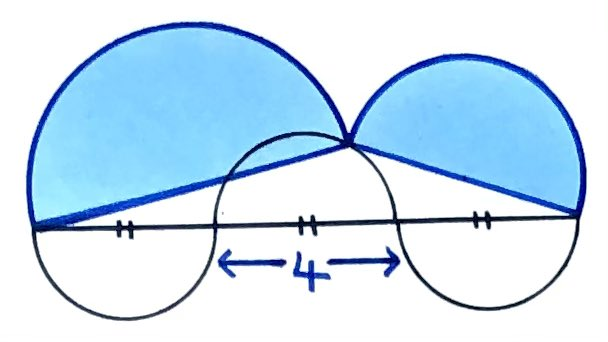
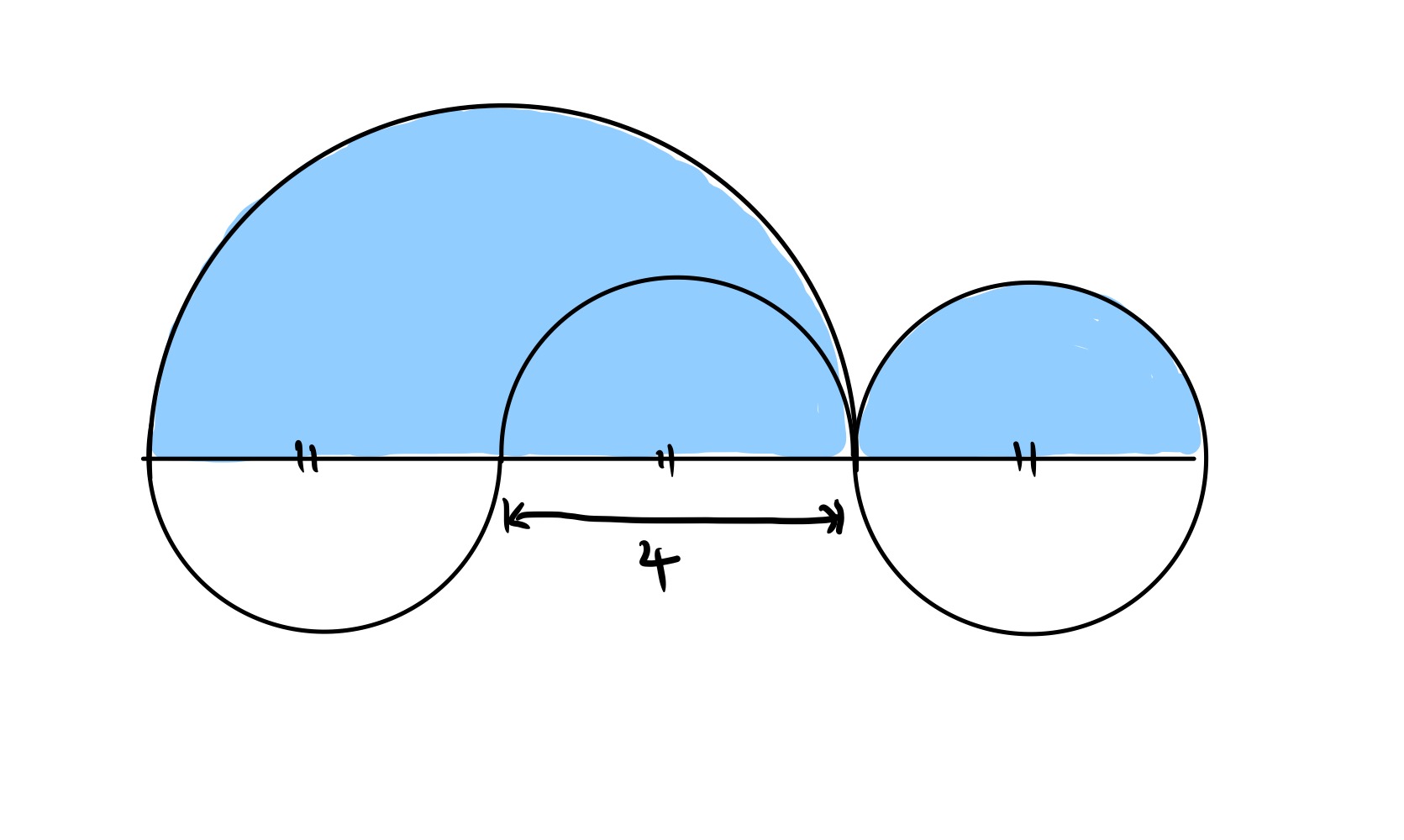
A design made from semicircles. What’s the total shaded area?
Solution by Pythagoras' Theorem
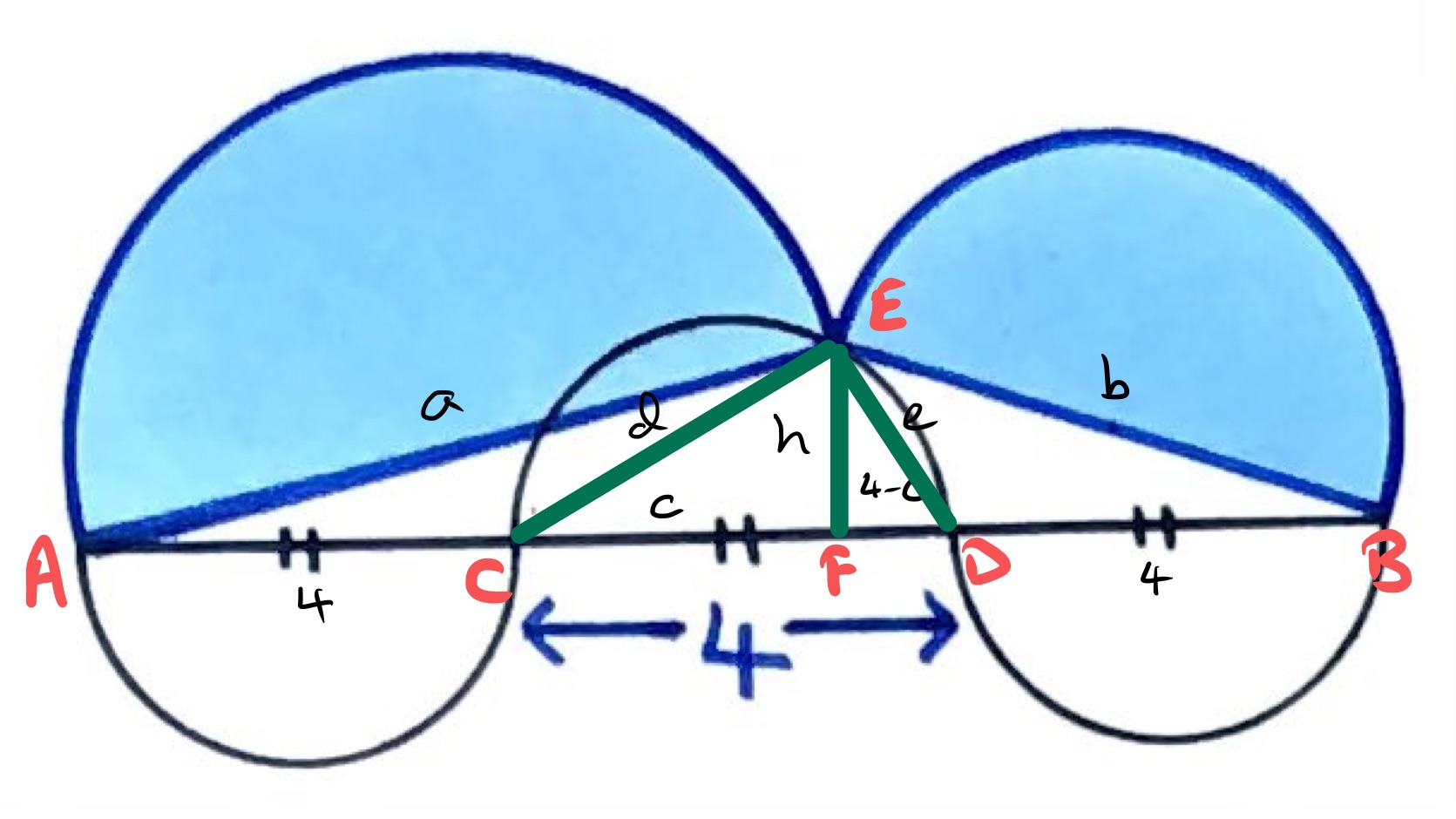
With the lengths labelled as in the above diagram, Pythagoras' theorem gives the following identities:
Putting some of these together leads to:
Combining these gets:
The area of a semi-circle of diameter is:
And so the areas of the semi-circles add to .
Solution by the Intersecting Chords Theorem
(With a smidgeon of Pythagoras' Theorem)
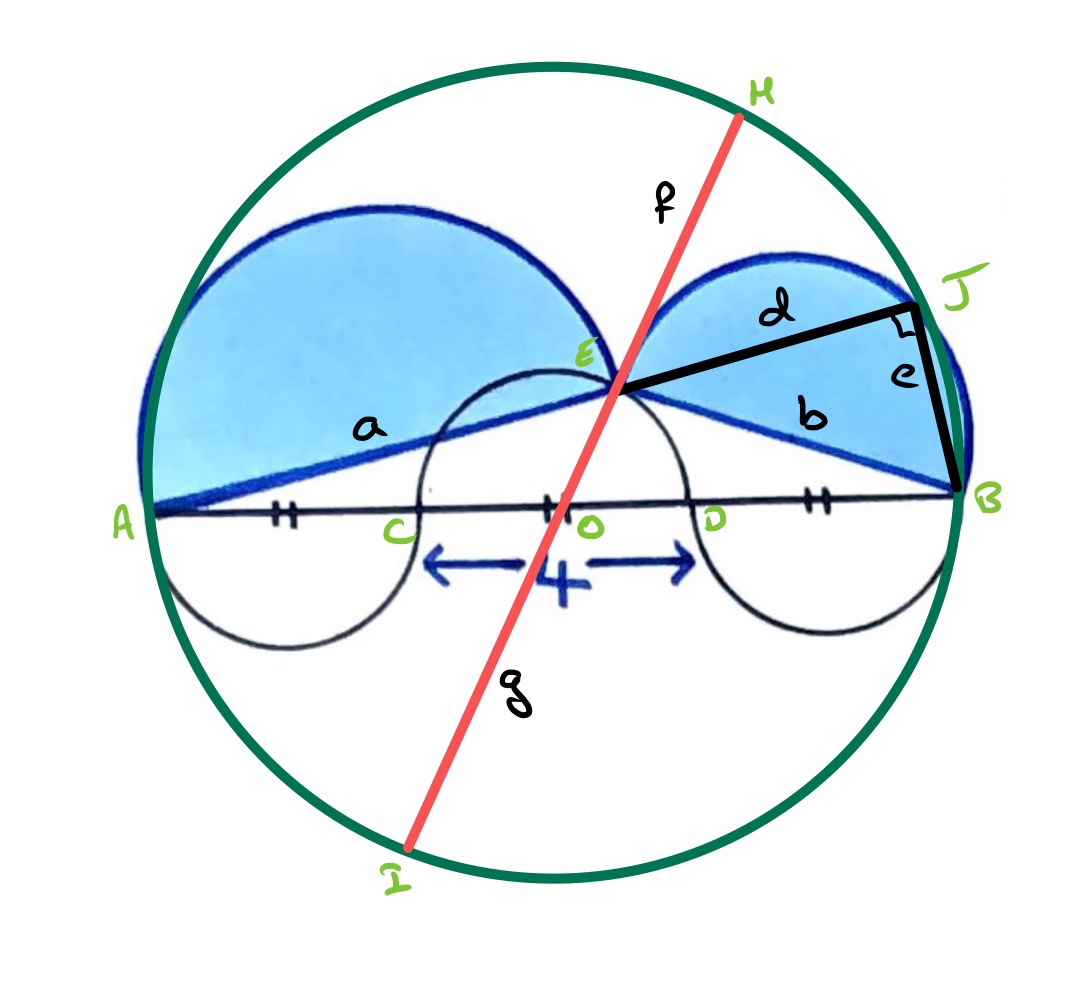
In the diagram above, the line segment is a diameter of the outer circle. As is on the middle circle, length and . The intersecting chords theorem then says that . Applying Pythagoras' theorem to the right-angled triangle yields the identity , and applying it to produces:
And so as before.
(Note: This method was inspired by the cosine rule and the invariance principle since if is constant then when applying the cosine rule to triangle the term has to be constant. In the above diagram, this is .)
Solution by the Parallelogram Law
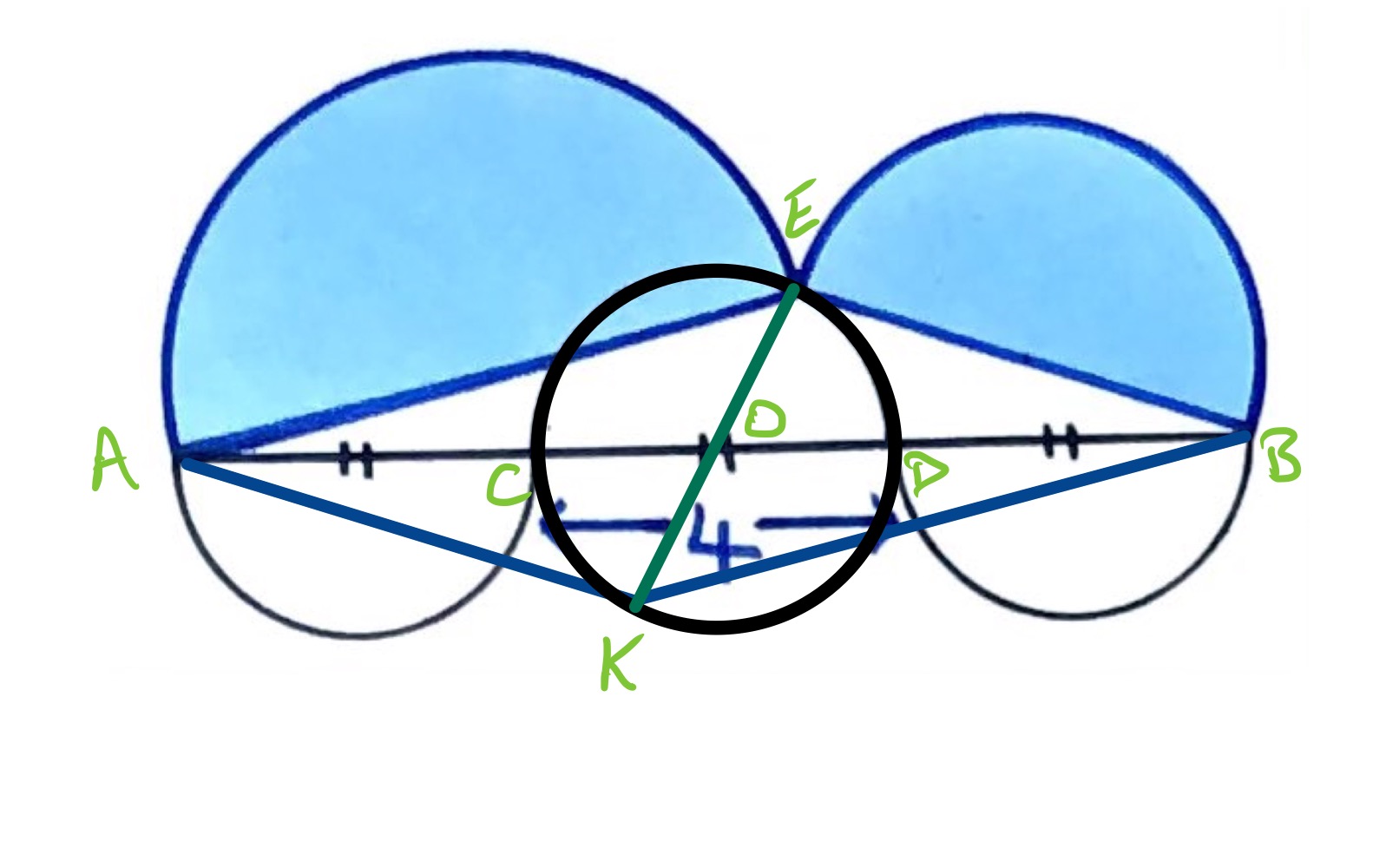
In the above diagram, is the point on the inner middle circle diametrically opposite to , so that is congruent to and to . So is a parallelogram. According to the parallelogram law,
Since and , this means that (with and as in above sections):
and the solution follows as before.
Solution by the Invariance principles
The point can move around on the circumference of the middle circle, and this leads to two special configurations.
The left-hand semi-circle has radius and the right-hand one has radius . So their areas are:
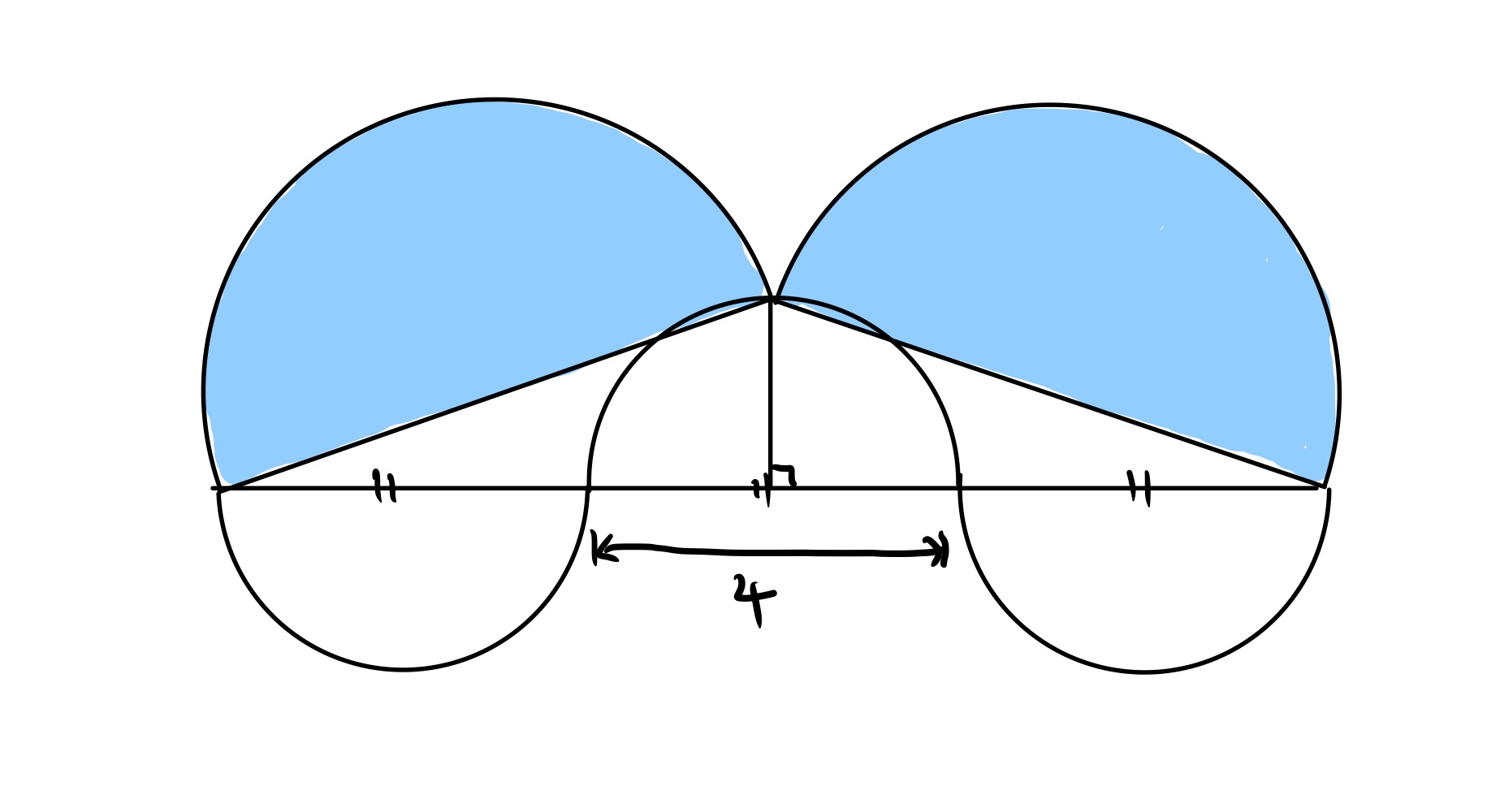
In this configuration, the diameter of each semi-circle is the hypotenuse of a triangle with other sides and , so its square is . The sum of the squares of the diameters is therefore which leads to the area of the semi-circles being as before.