Notes
five semi-circles around a rectangle solution
Five Semi-Circles Around a Rectangle
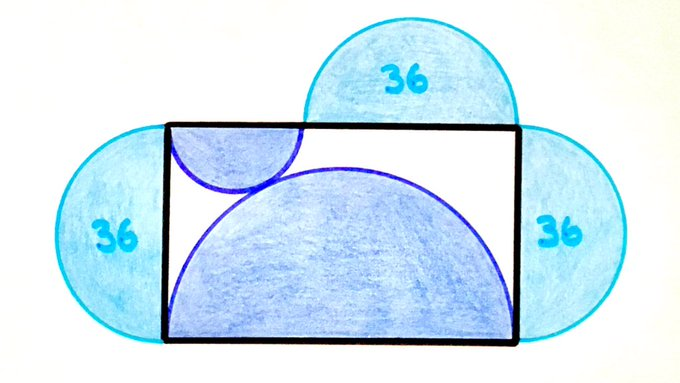
Three of these semicircles have area . What’s the total area of the other two?
Solution by Pythagoras' Theorem and Area of a Circle
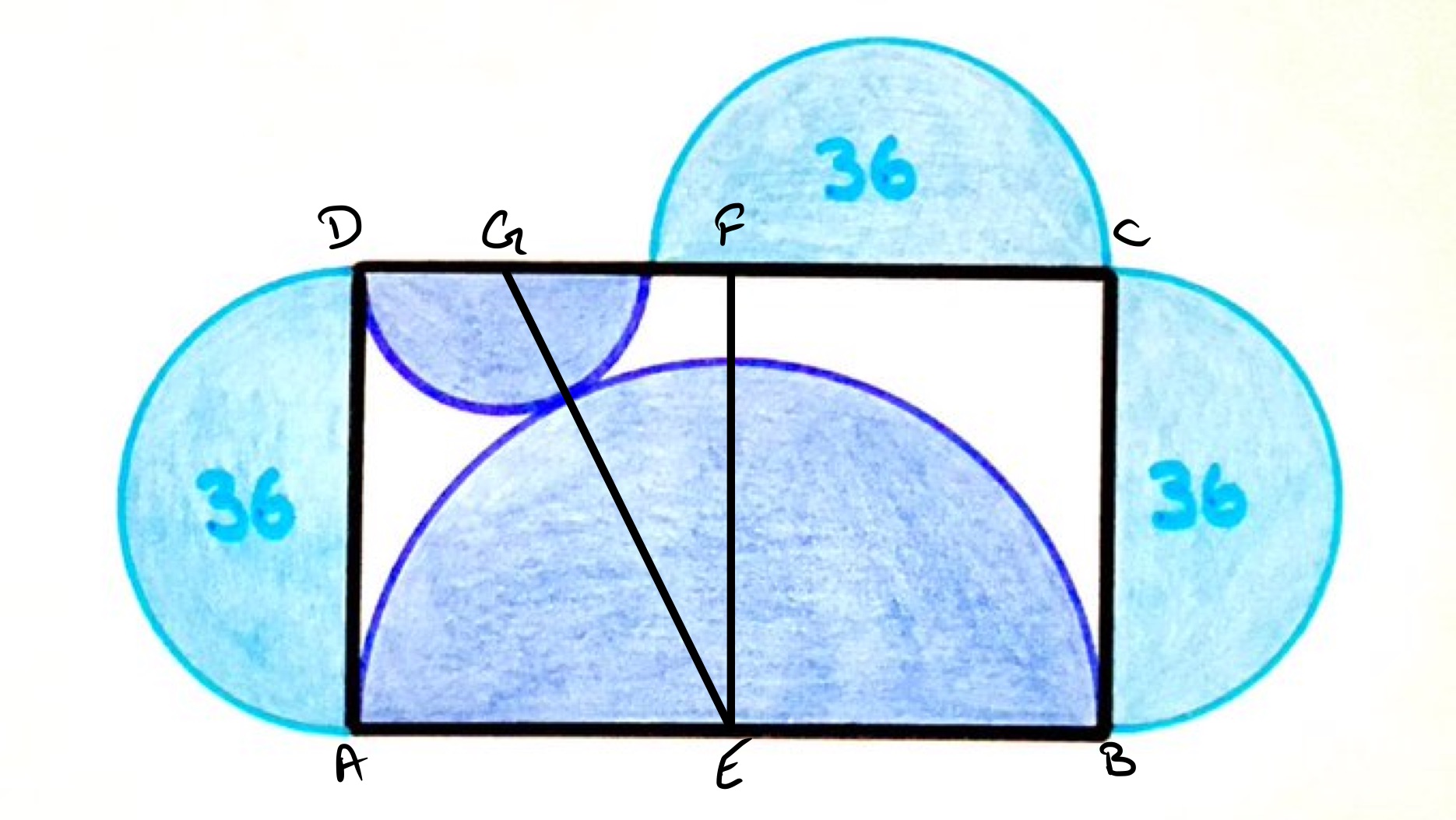
In the above diagram, point is the midpoint of and so is the centre of the largest semi-circle. Point is the midpoint of , and point is the centre of the smallest semi-circle.
Let be the radius of the largest semi-circle, of the smallest, and of the three semi-circles with area . Then .
As the lengths of and are the same, . The length of is half this, so is , and then the length of is . The length of is , and of is . Applying Pythagoras' theorem to triangle shows that:
Rearranging the identity yields and so . So combining this with the above gives:
The total area of the purple semi-circles is therefore: