Notes
five rectangles in a square solution

Five Rectangles in a Square

Solution by Lengths in a Square

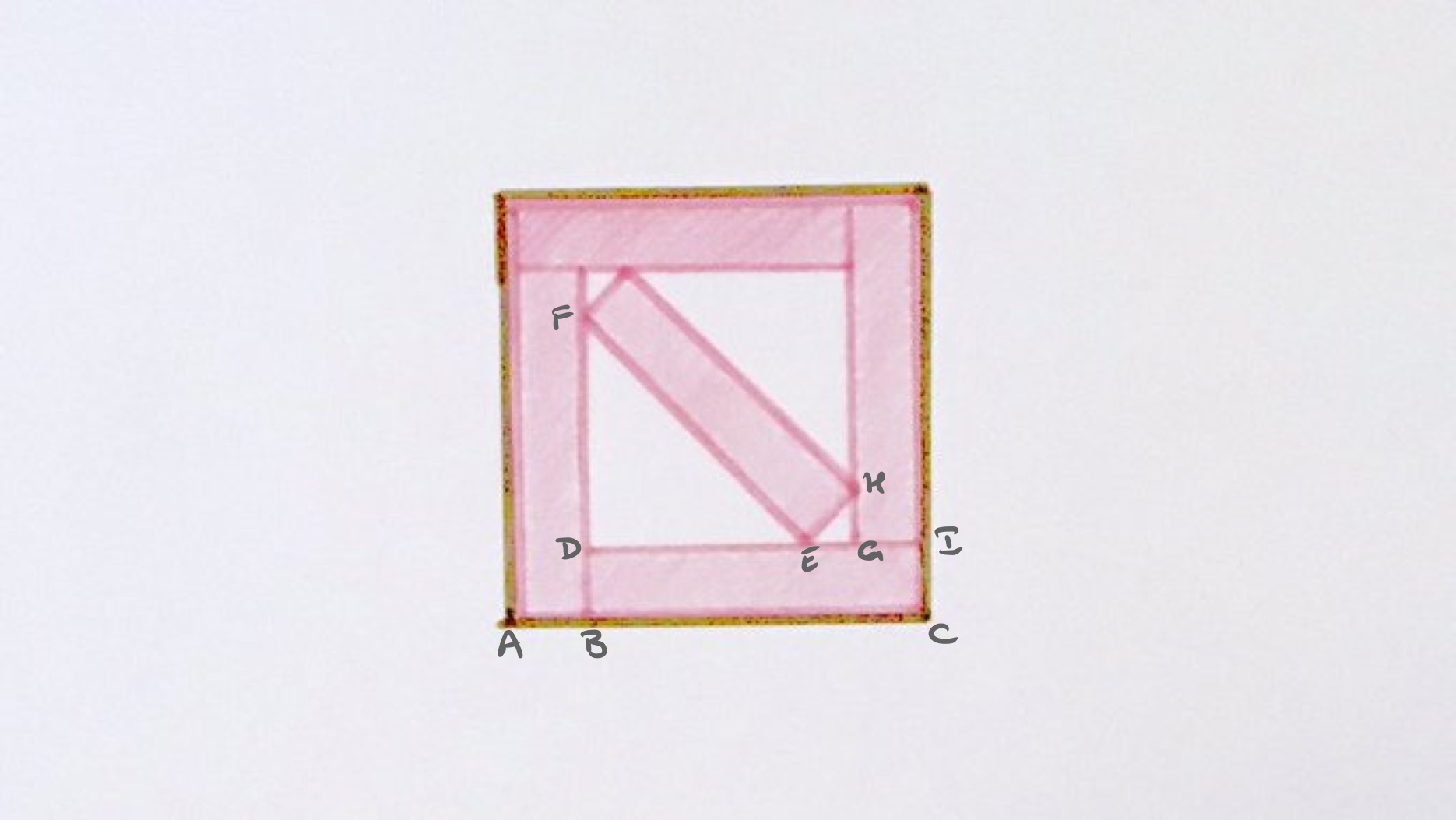
Let the sides of the rectangle be $a$ and $b$, with $b$ the short side and $a$ the long. The side of the outer square is then $a + b$ so its area is $(a + b)^2$. Each rectangle has area $a b$, so the fraction of the square covered by the rectangles is:

Triangle $F D E$ is an isosceles right-angled triangle so the length of $F E$ is $\sqrt{2}$ times the length of $D E$. Similarly, the length of $E H$ is $\sqrt{2}$ times the length of $E G$. Since $F E$ has length $a$ and $E H$ has length $b$, the sum of these lengths is $a + b$ and this is $\sqrt{2}$ times the length of $D G$, which is $a - b$. That is to say, $a + b = \sqrt{2}(a - b)$. Squaring both sides shows that:

So the fraction of the square covered by the rectangles is $\frac{5}{8}$.