Notes
five quarter circles solution
Solution to the Five Quarter Circles Puzzle
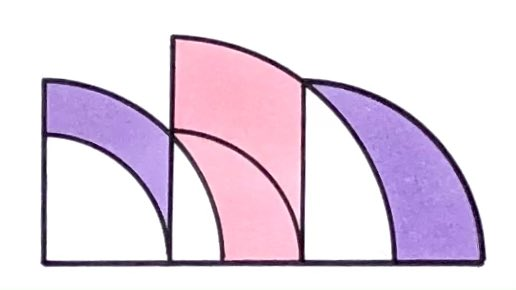
This design is made of quarter circles. Is more of it shaded pink or purple?
Solution by Circle Areas and Pythagoras' Theorem
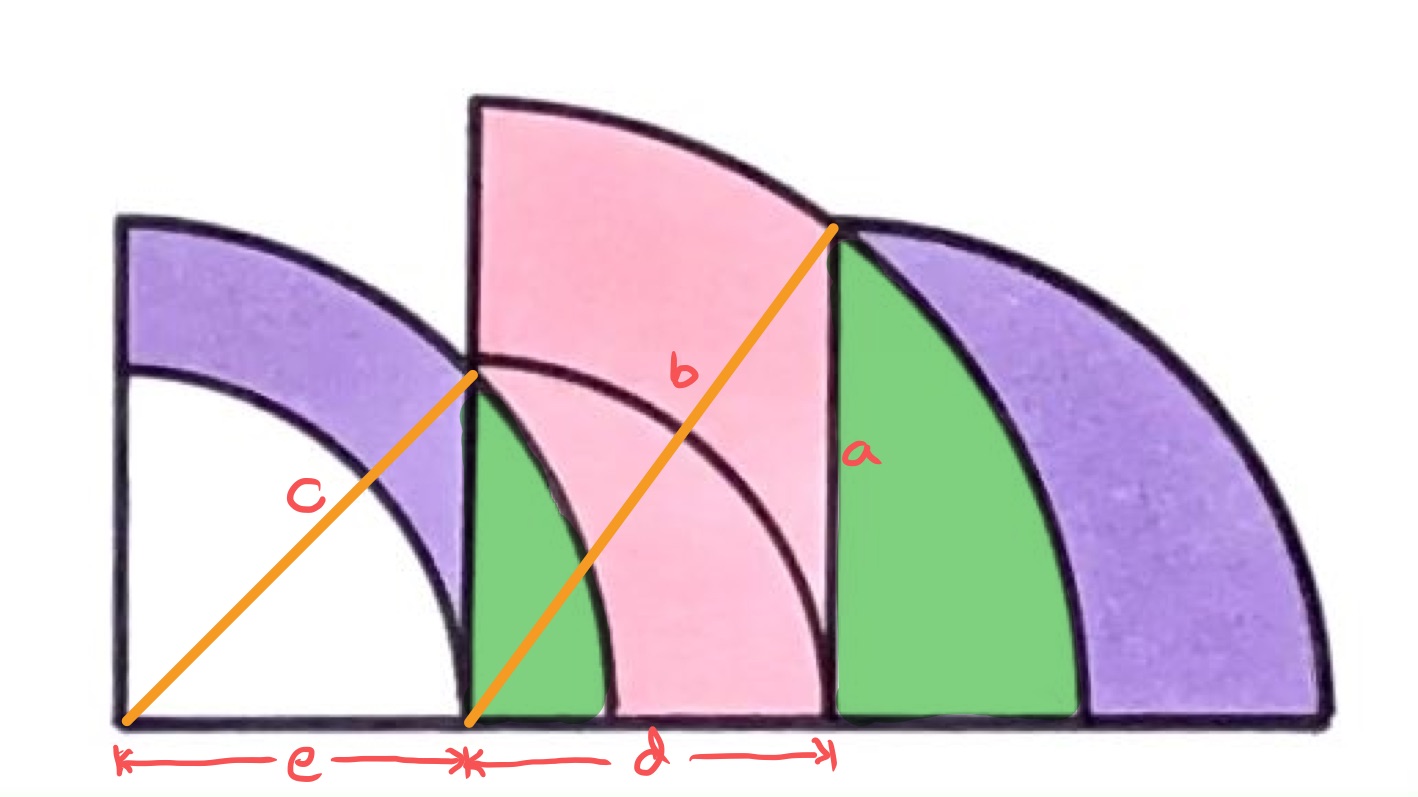
It is the same question to determine the relative sizes of the pink and purple areas as when the green areas are included with both the pink and purple. This completes the shapes to ones built out of quarter circles.
With the lengths labelled as above, the purple (and green) regions have area given by:
The pink (and green) regions have area given by:
From Pythagoras' theorem, the various lengths are related by:
Eliminating from these two yields:
Multiplying through by shows that the pink and green region is the same area as the purple and green, and so the pink and purple regions are the same area.