Notes
five overlapping circles solution

Five Overlapping Circles

Solution by Pythagoras' Theorem

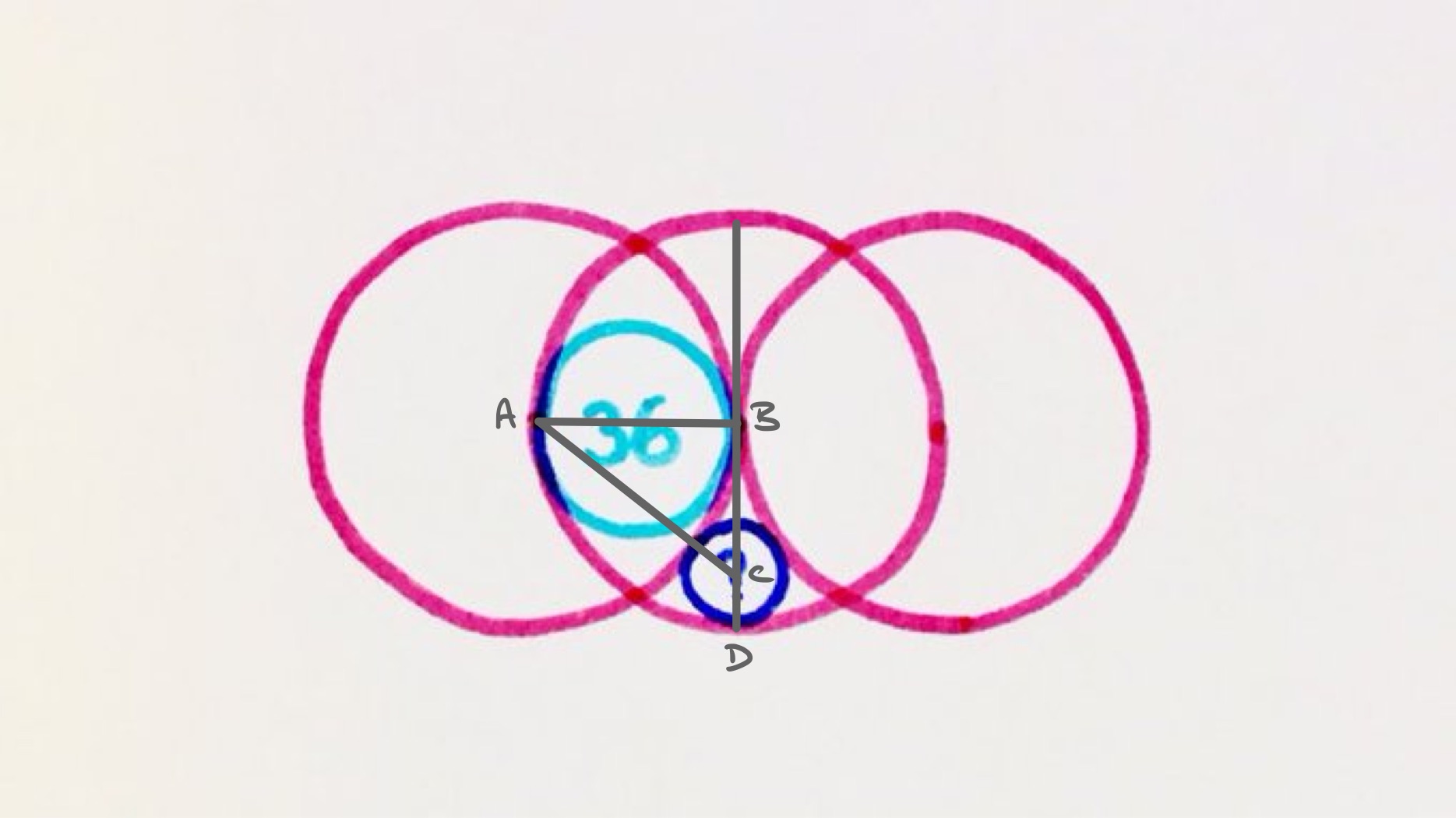
Let $a$ be the radius of the cyan circle and $b$ of the dark blue. Then the length of $A B$ is $2 a$, of $B C$ is $2 a - b$, and of $A C$ is $2 a + b$. Applying Pythagoras' theorem to triangle $A B C$ shows that:

This simplifies to $8 a b = 4 a^2$, so $a = 2 b$. This means that the area of the small circle is a quarter of the area of the cyan circle, so has area $9$.