Notes
five equilateral triangles solution

Solution to the Five Equilateral Triangles Puzzle

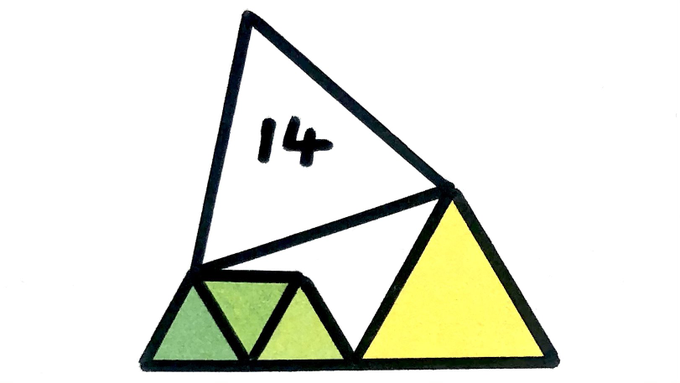
Five Equilateral Triangles

The largest of these equilateral triangles has area $14$ . What’s the total area of the other four?

Solution by Pythagoras' Theorem

First Version

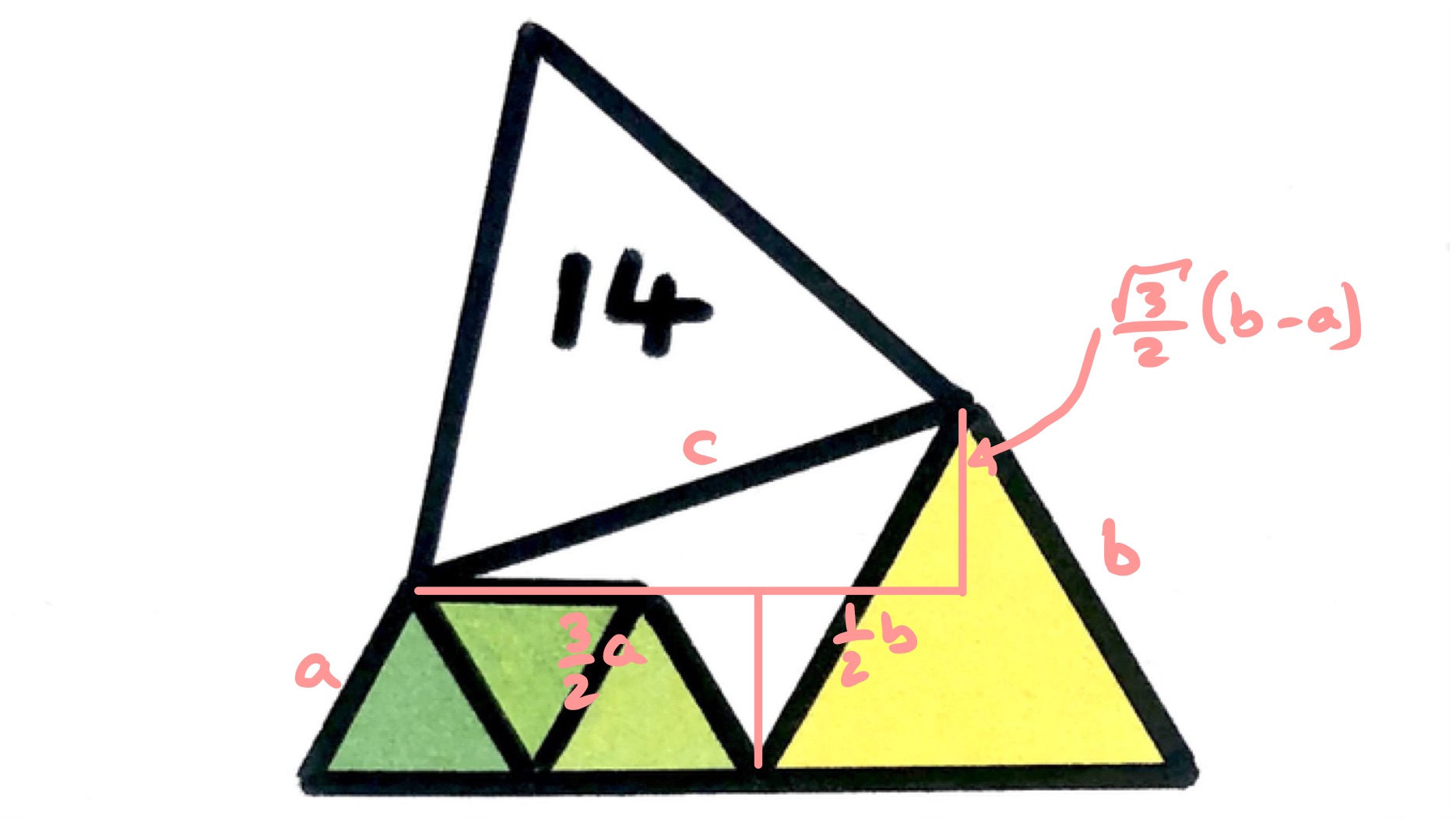
Five equilateral triangles first version with Pythagoras

In the first solution using Pythagoras' Theorem, the right-angled triangle has horizontal and vertical sides and the hypotenuse is the base of the upper triangle, as in the above diagram.

Let $a$ be the side length of the smallest equilateral triangle, $b$ of the middle triangle, and $c$ of the largest (that has area $14$ ). The base of the right-angled triangle is then $\frac{3}{2} a + \frac{1}{2} b$ . The height is the difference of the heights of the two smaller triangles, which is $\frac{\sqrt{3}}{2} (b - a)$ (using that the height of an equilateral triangle is $\frac{\sqrt{3}}{2}$ times the side length).

Applying Pythagoras' Theorem to the right-angled triangle, we get:

\begin{aligned} c^2 &= \left( \frac{3}{2} a + \frac{1}{2} b \right)^2 + \left( \frac{\sqrt{3}}{2} (b - a) \right)^2 \\ &= \frac{9}{4} a^2 + \frac{3}{2} a b + \frac{1}{4} b^2 + \frac{3}{4} (b^2 - 2 a b + a^2) \\ &= 3 a^2 + b^2 \end{aligned}

The area of an equilateral triangle with side length $x$ is $\frac{\sqrt{3}}{2} x^2$ , so using the above equation the areas of the four triangles is:

3 \frac{\sqrt{3}}{2} a^2 + \frac{\sqrt{3}}{2} b^2 = \frac{\sqrt{3}}{2} c^2 = 14

Second Version

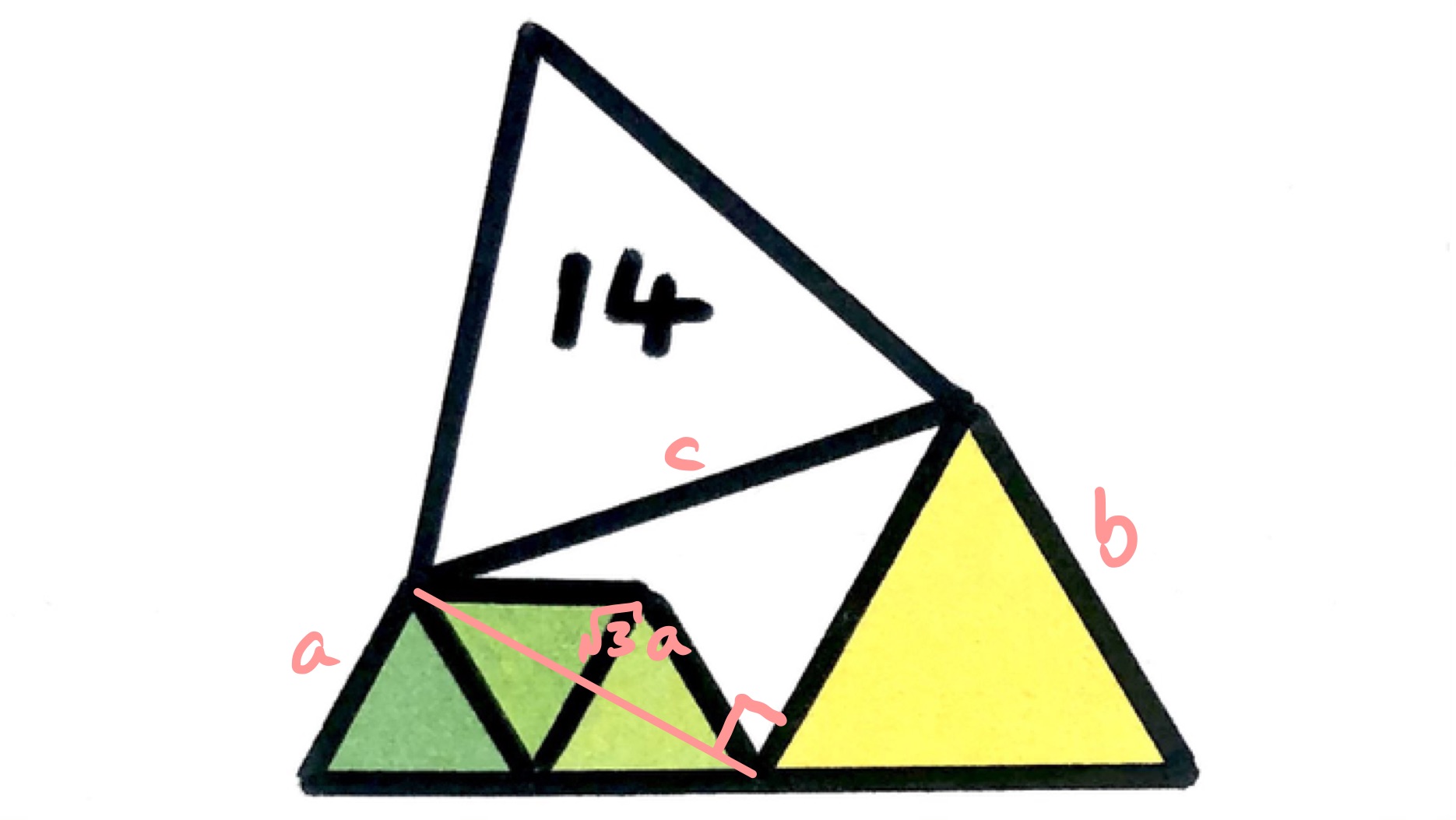
Five equilateral triangles second Pythagoras version

In the second version that uses Pythagoras' theorem, the right-angled triangle is formed by taking the left-hand side of the middle sized triangle and joining that to the base of the largest triangle. This cuts through two of the smallest triangles.

The angle at the bottom is a right-angle as it comprises $60^\circ + \frac{1}{2} \times 60^\circ = 90^\circ$ .

The height of an equilateral triangle is $\frac{\sqrt{3}}{2}$ times its side length, so the length of the line that cuts through the smallest triangles is $\sqrt{3} a$ . Applying Pythagoras' Theorem we get:

c^2 = b^2 + (\sqrt{3} a)^2 = b^2 + 3 a^2

As above, this means that the areas of the four smaller triangles is the same as that of the largest triangle, that is $14$ .

Solution by Invariance Principle

The two special cases of this problem as when the right-hand triangle is the same size as the others, and when it is as large as possible.

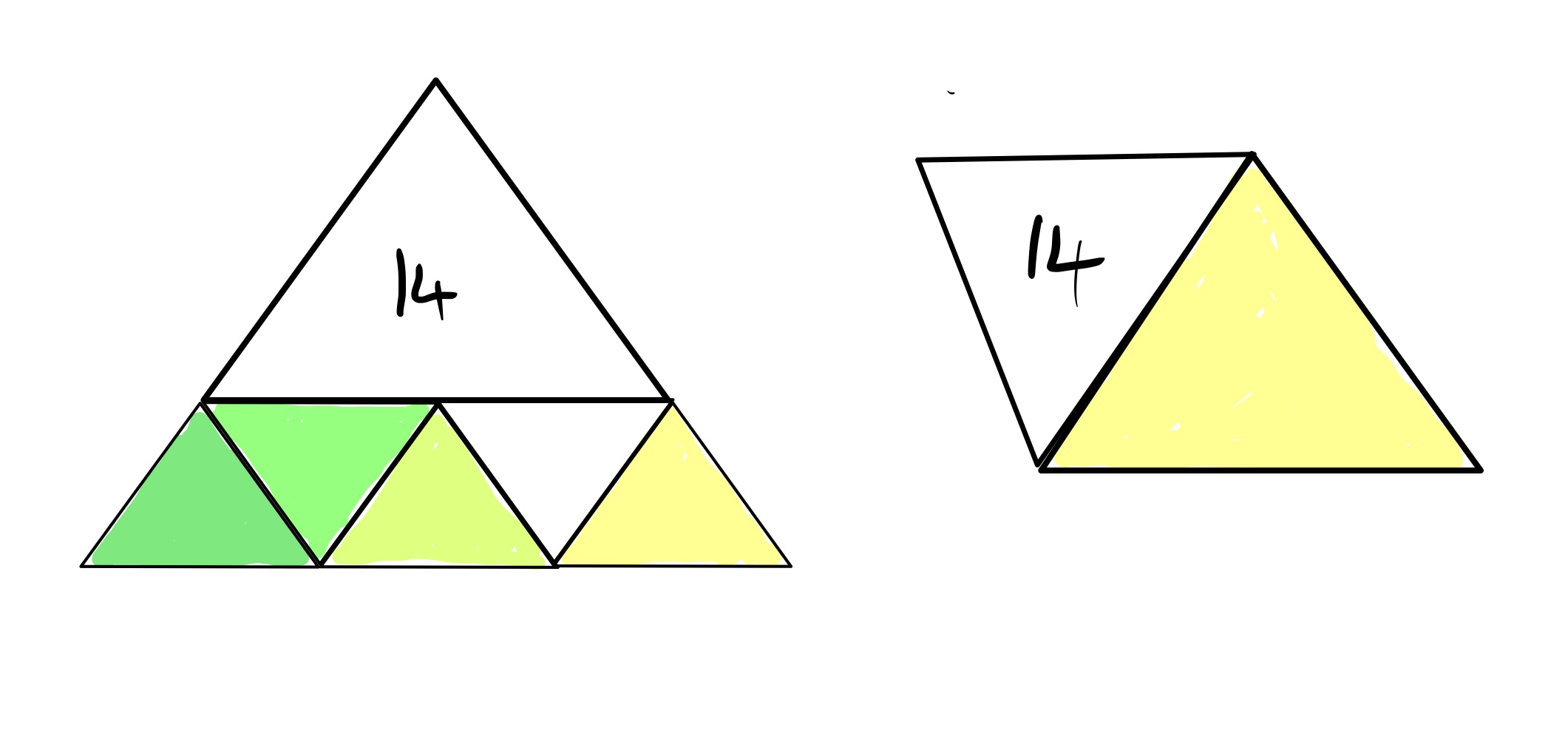
Five equilateral triangles extreme versions

When all the coloured triangles are the same size, the side length of these is half that of the largest triangle, and so the areas of these is a quarter of the area of the largest triangle. Since there are four of them, the overall areas are the same.

When the right-hand triangle is as large as possible, the other three triangles have no size and the yellow triangle is exactly the same size as the largest triangle, hence the total area is $14$ .