Notes
five decreasing squares solution
Solution to the Five Decreasing Squares Puzzle
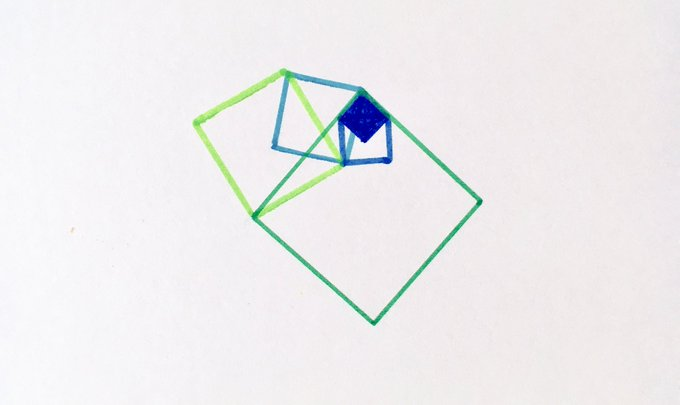
What fraction of the largest square is shaded?
Solution by Dissection
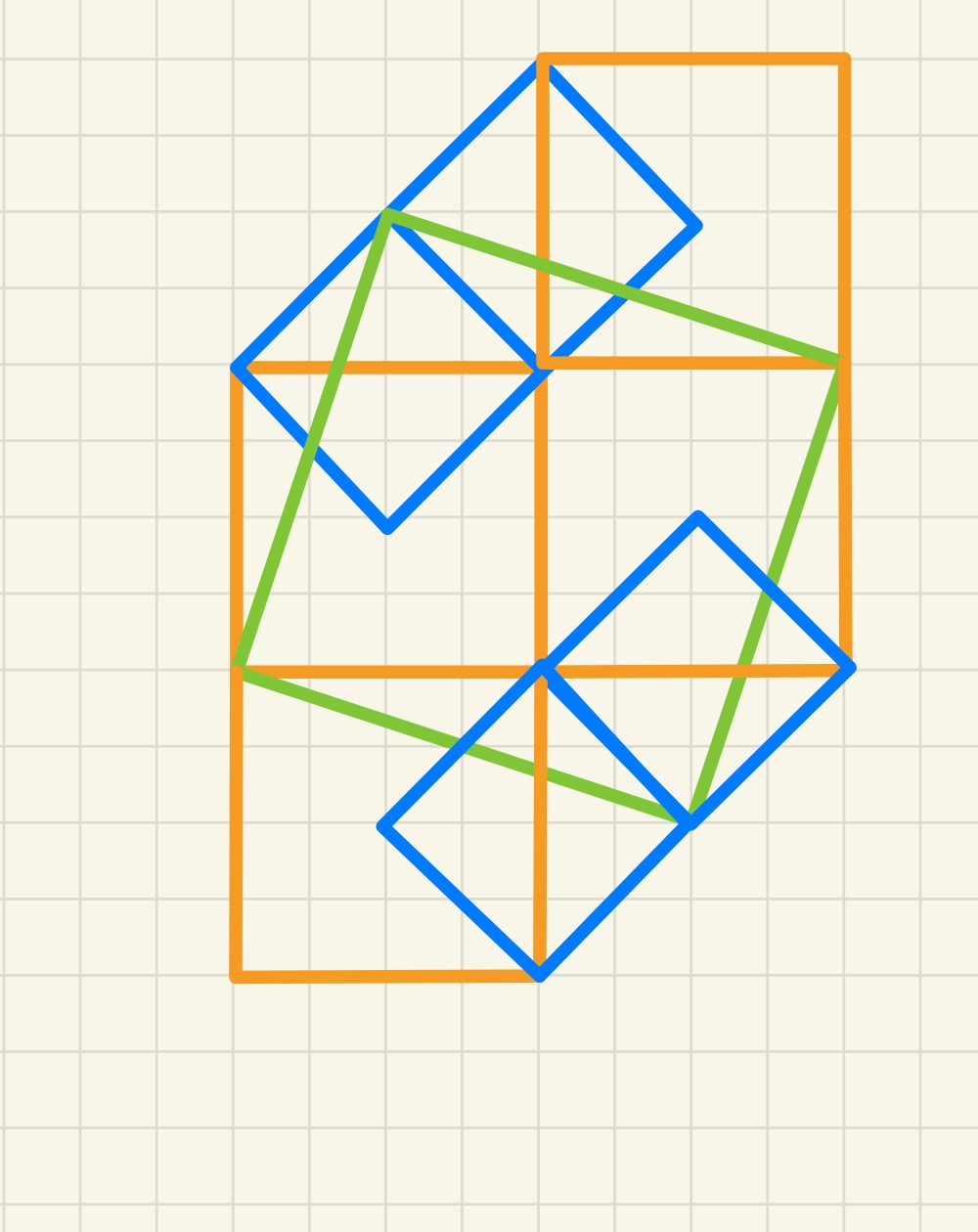
In the above picture, the area of the orange square is twice the area of the blue square while the area of the green square is twice the area of one orange square and half a blue square. So the orange square has area five times that of the blue square. Therefore in the original puzzle the largest square has area twenty-five times that of the smallest.
Solution by Pythagoras’ Theorem
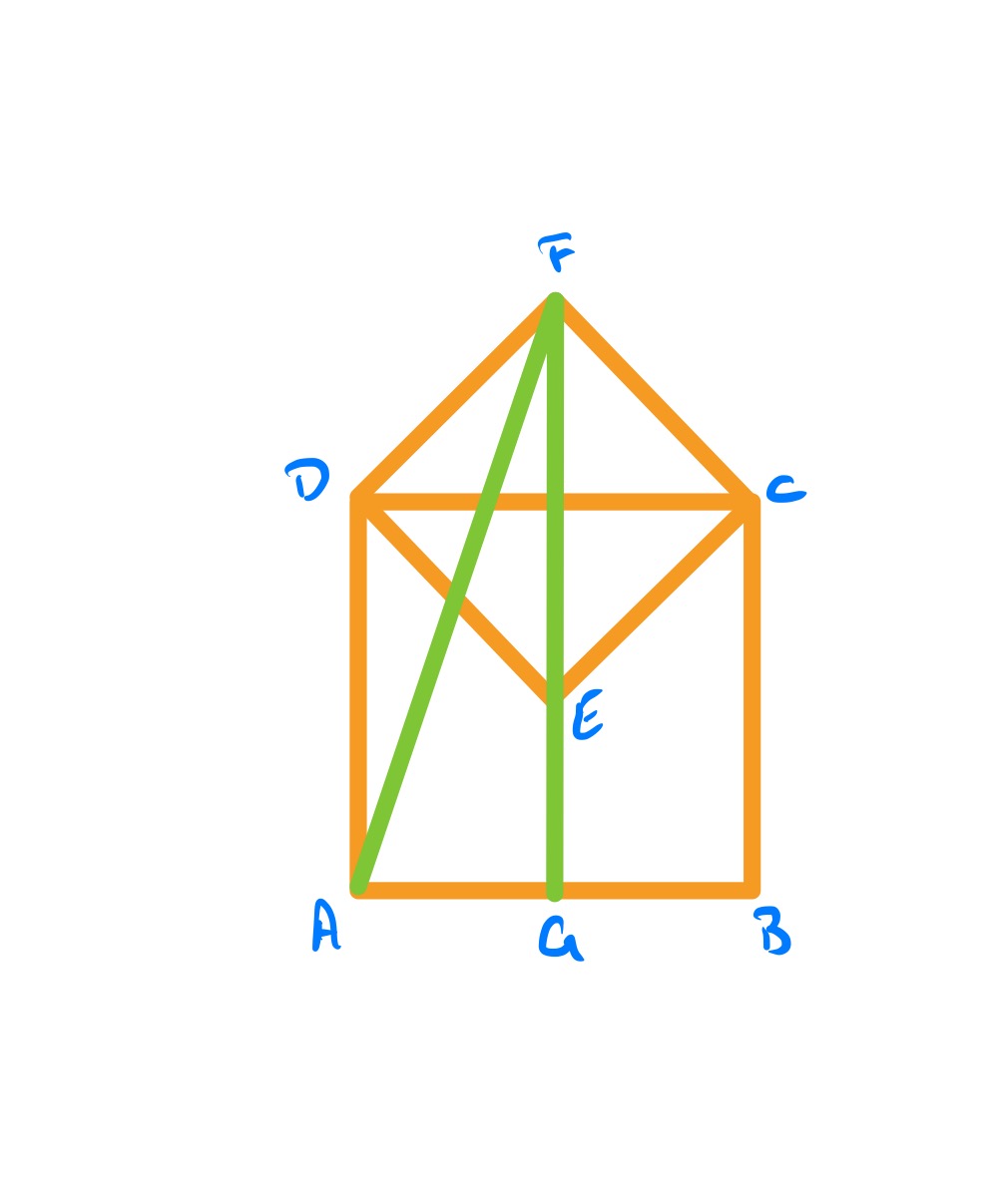
With the points labelled as above, let be the length of , the length of , and of . Then has length and has length so applying Pythagoras’ Theorem to triangle shows that
Applying Pythagoras’ Theorem to triable then shows that . Putting those together yields .
This ratio occurs twice in the main diagram, so the area of the largest square is twenty-five times that of the smallest.