Notes
five circles in a square solution

Solution to the Five Circles in a Square Puzzle

Solution by Trigonometry and Lengths in an Equilateral Triangle

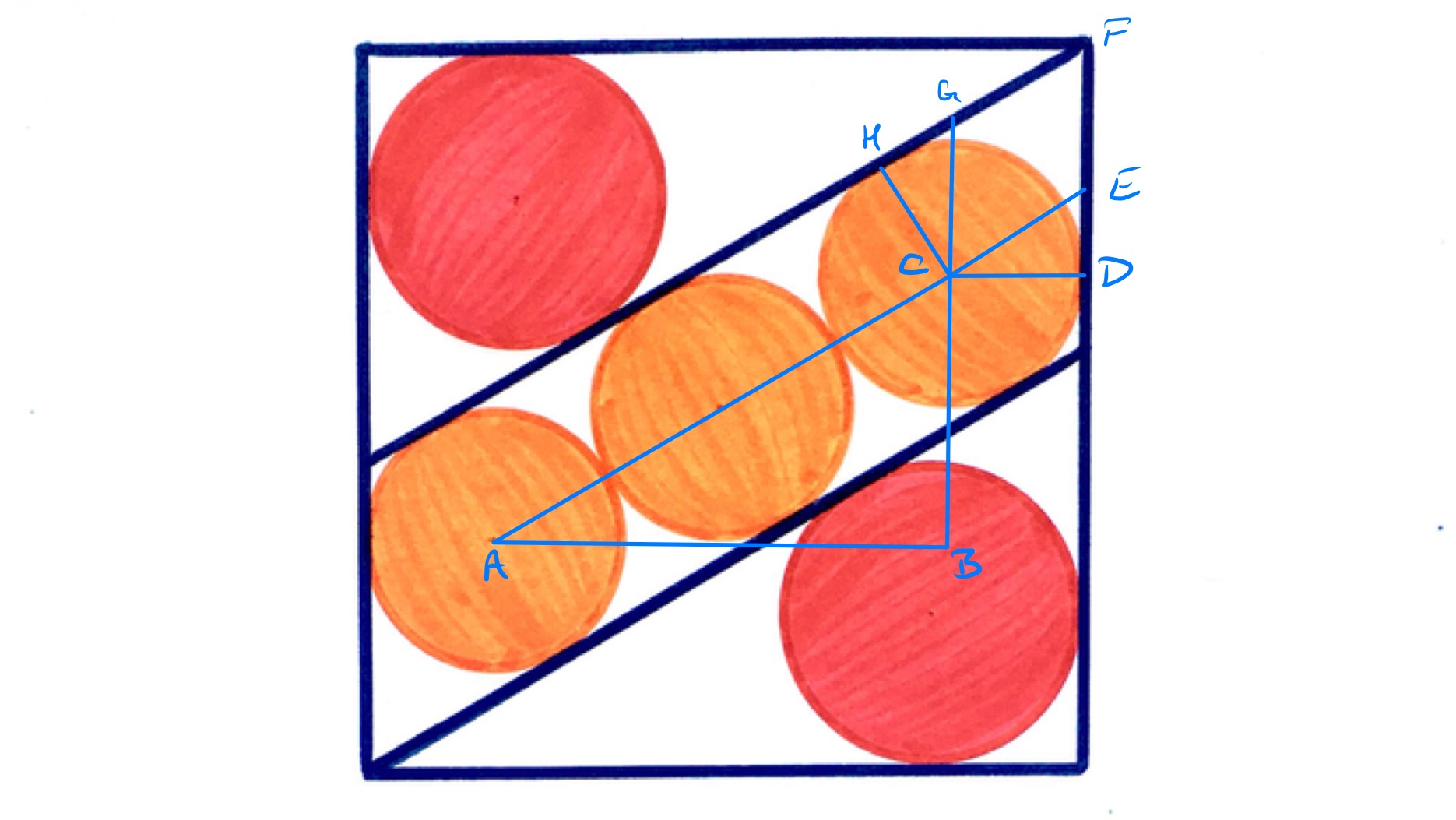
In the above picture, let $r$ be the radius of the orange circles. The points $A$ and $C$ are centres of their circles and $B$ is so that $A B$ is horizontal and $B C$ is vertical. Let $\alpha$ be angle $B \hat{A} C$.

The length of the line segment $A C$ is $4 r$, so $C B$ has length $4 r \sin(\alpha)$ and $A B$ has length $4 r \cos(\alpha)$. Since $C D$ has length $r$, the horizontal length of the square is $2 r + 4 r \cos(\alpha)$.

As $C D$ has length $r$, $E D$ has length $r \tan(\alpha)$ and $E C$ has length $r \sec(\alpha)$. So the total height of the square is $2 r \sec(\alpha) + 2 r \tan(\alpha) + 4 r \sin(\alpha)$.

Since it is a square, these two expressions must be equal. Setting them equal and working through goes as follows:

The last step uses the compound angle formula with one of the angles set to $45^\circ$ together with the fact that $\sin(45^\circ) = \cos(45^\circ)$.

This has solutions $2 \alpha - 45^\circ = 45^\circ - \alpha + 360^\circ k$ and $2 \alpha - 45^\circ = 180^\circ - (45^\circ - \alpha) + 360^\circ k$, where $k$ is some integer. The first rearranges to $3 \alpha = 90^\circ + 360^\circ k$, so $\alpha = 30^\circ + 120^\circ k$, and the second to $\alpha = 180^\circ + 360^\circ k$. Since $\alpha$ is acute, the only solution is $\alpha = 30^\circ$.

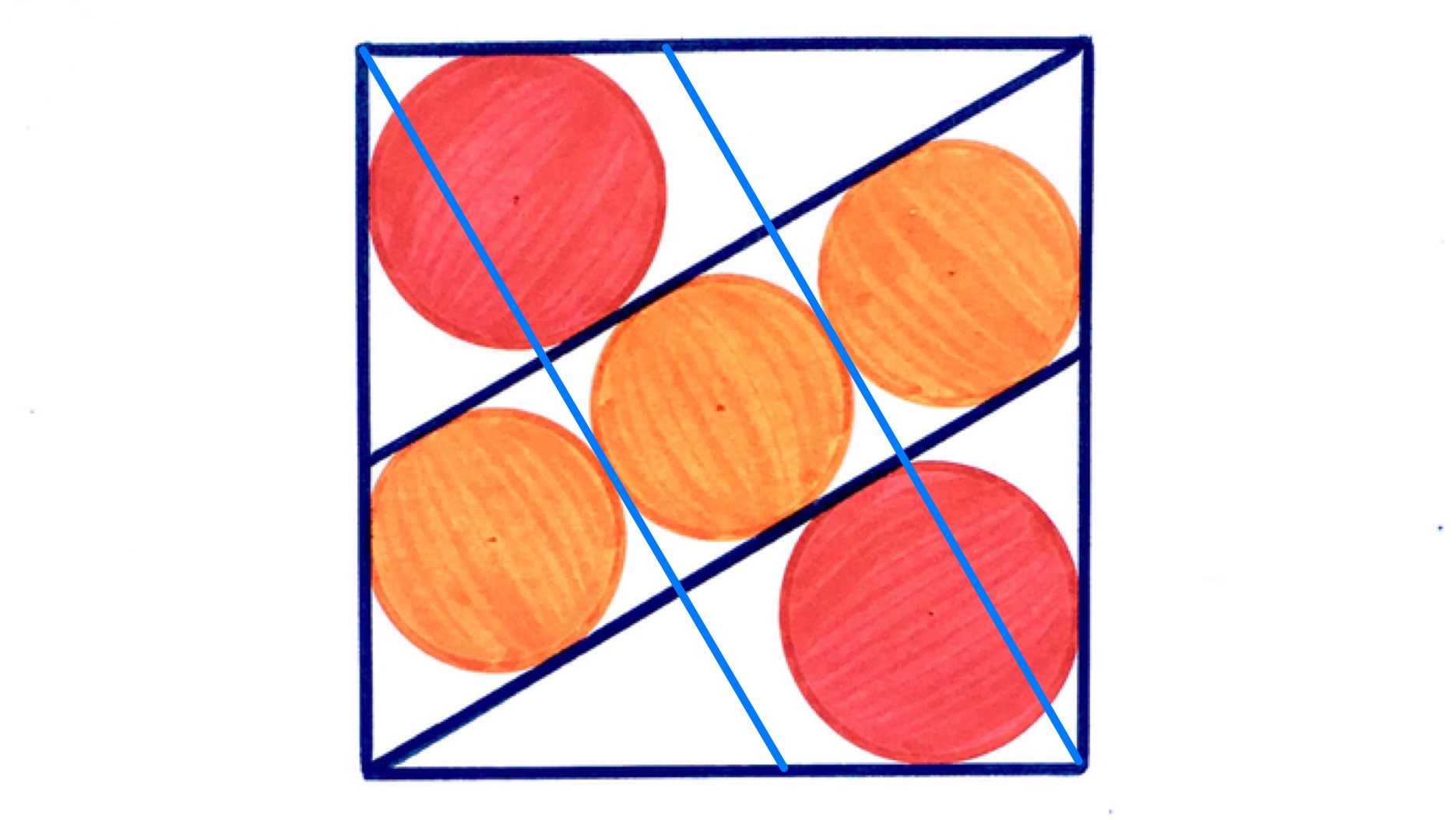
With $\alpha$ established as $30^\circ$, the above diagram shows the relationship between the orange and red circles. Each is the incircle of a $30^\circ$-$60^\circ$-$90^\circ$ triangle, with the side adjacent to $\alpha$ on the larger circle being the hypotenuse of the smaller. The length scale factor is therefore the ratio of the length of the hypotenuse to the length of that side, which from lengths in an equilateral triangle is $\frac{\sqrt{3}}{2}$. So the area scale factor is $\frac{3}{4}$. That is, the area of each orange circle is $\frac{3}{4}$ that of the red. Since the total red area is $24$, each red circle is $12$ and thus each orange circle is $9$ meaning that the total orange area is $27$.