Notes
equilateral triangles in a square solution

Equilateral Triangles in a Square

Solution by Lengths in an Equilateral Triangle

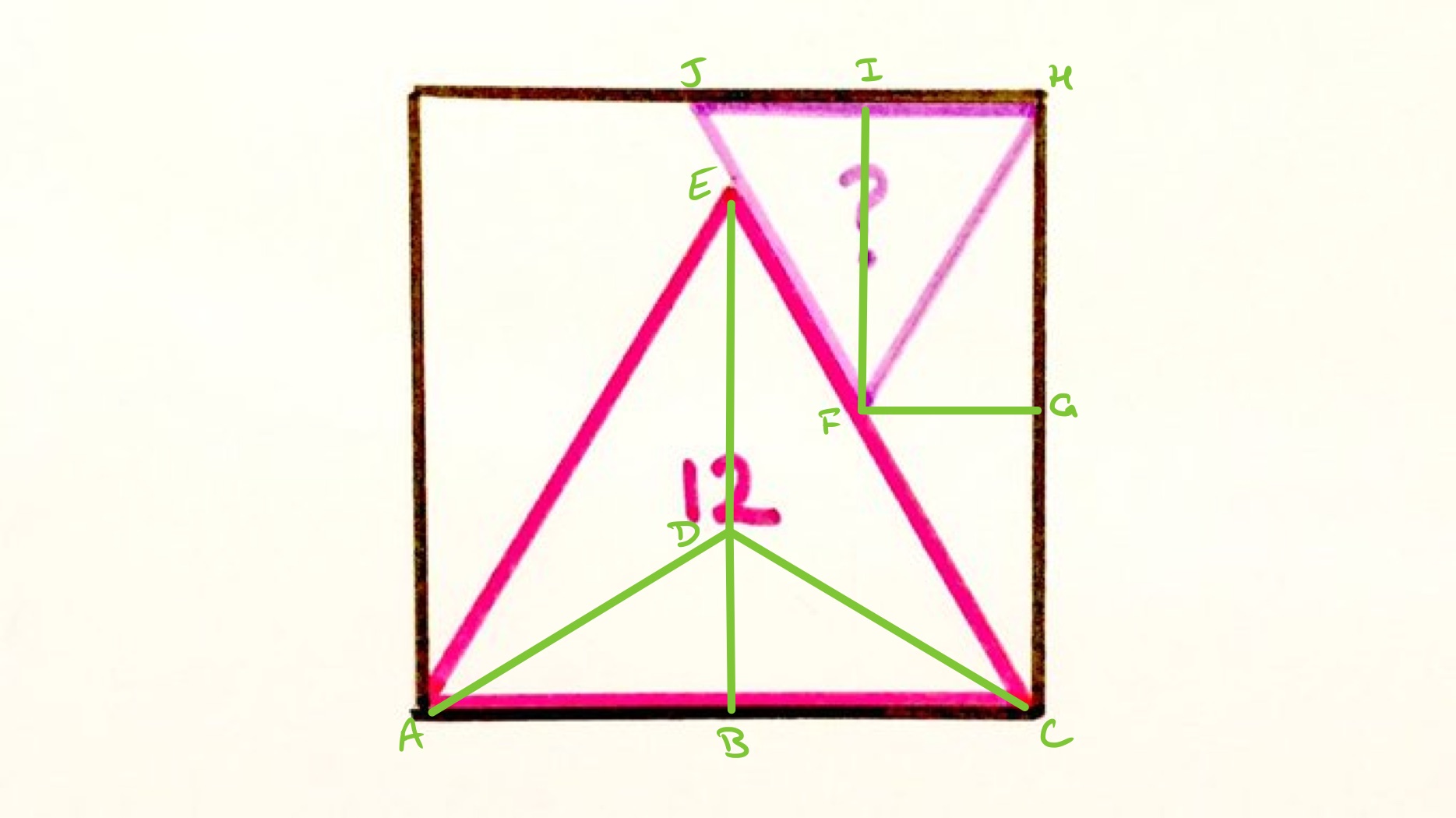
In the above diagram, $D$ is the circumcentre of the equilateral triangle, so $D A$, $D C$, and $D E$ all have the same length. Angles $C \hat{A} D$ and $D \hat{C} A$ are both $30^\circ$.

Angles $H \hat{C} F$ and $F \hat{H} C$ are both $90^\circ - 60^\circ = 30^\circ$, then $A C$ and $C H$ have the same length as they are both sides of the square. So triangles $A D C$ and $C F H$ are congruent. This means that the length of $F H$ is the same as that of $C D$, and so of $E D$.

Using the relationships between lengths in an equilateral triangle, $E D$ is $\frac{2}{3}$rds of $E B$, and $E B$ is $\frac{\sqrt{3}}{2}$ of $A C$. So the side length of the smaller triangle is $\frac{1}{\sqrt{3}}$ of the side length of the larger. Its area is therefore $\frac{1}{3}$rd of the area of the larger, and so is $4$.