Notes
divided square solution
Solution to the Divided Square Puzzle
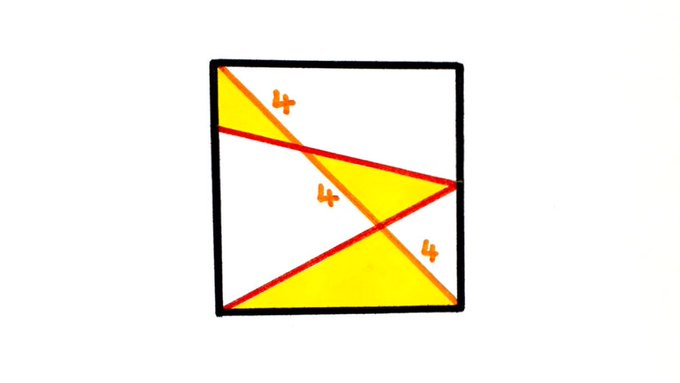
The diagonal of the square has been divided into three sections of length . What’s the total shaded area?
Solution by Area of a Triangle and Vertically Opposite Angles
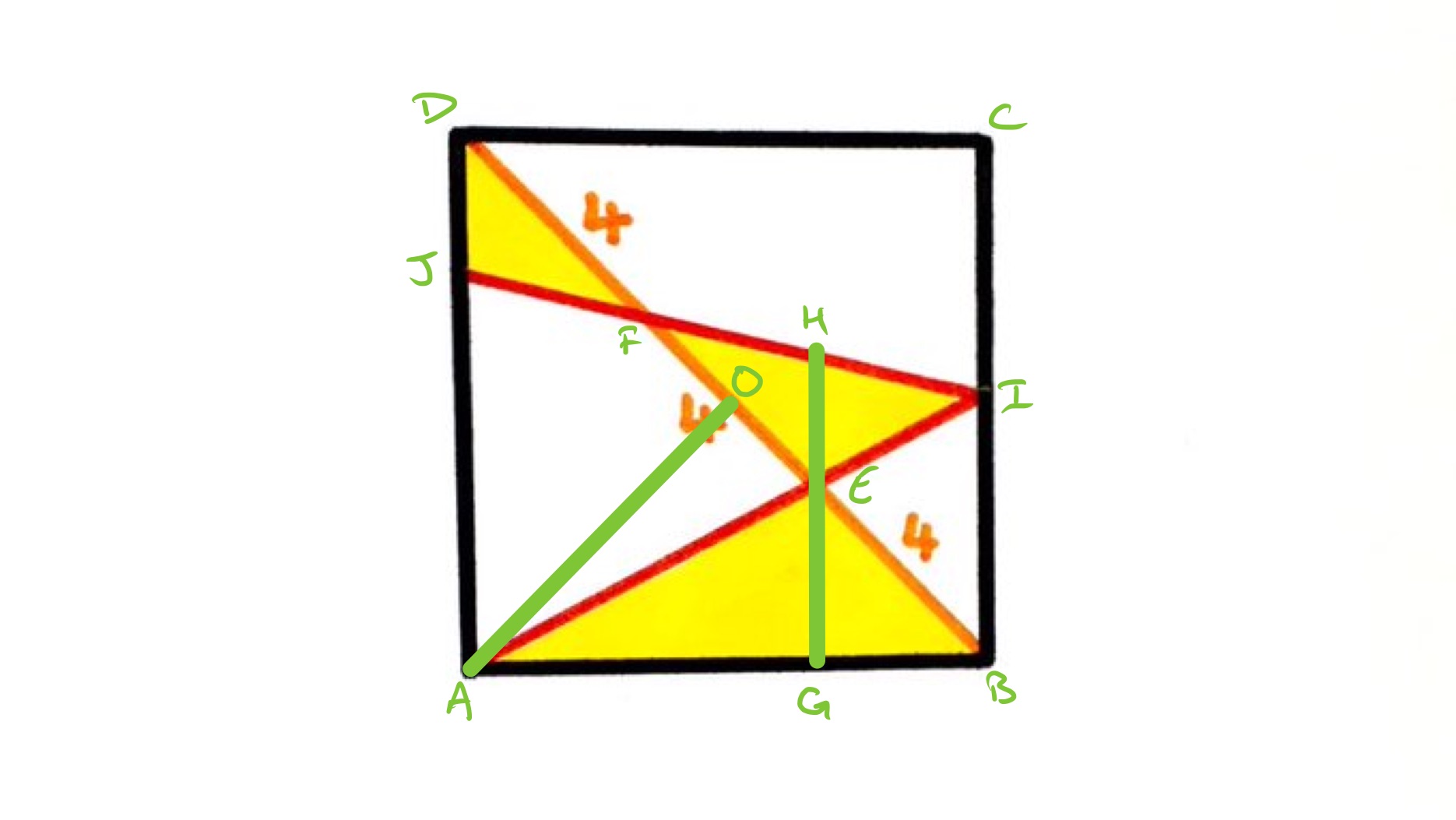
With the points labelled as above, consider first triangle . The length of is given as . The height of above is the length of , which is half a diameter and so is . Therefore the area of triangle is .
Since is rds of the way along , is also rds of the way along , so is half the length of . As angles and are equal, since they are vertically opposite, the height of above is then half the height of above , so the area of is half that of , so is .
The line is vertical through , and so as is the midpoint of , is the midpoint of . This means that triangle has half the area of triangle , so has area . Then angles and are equal as they are vertically opposite and is parallel to and and are the same length, so triangles and are congruent. Hence triangle has area .
The shaded region therefore has area .