Notes
diagonal in a square solution
Diagonal in a Square
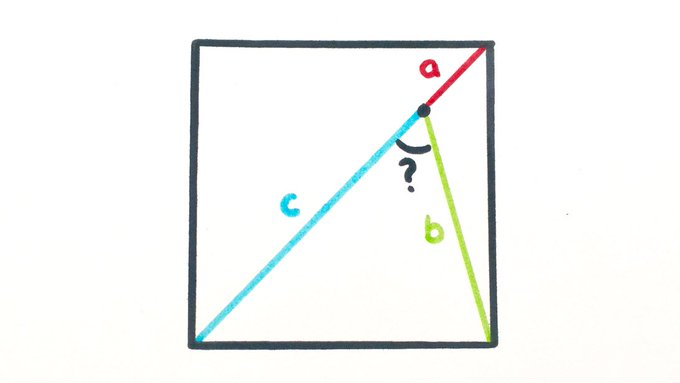
The point lies on the diagonal of the square so that . What’s the angle?
Solution by Equilateral Triangles
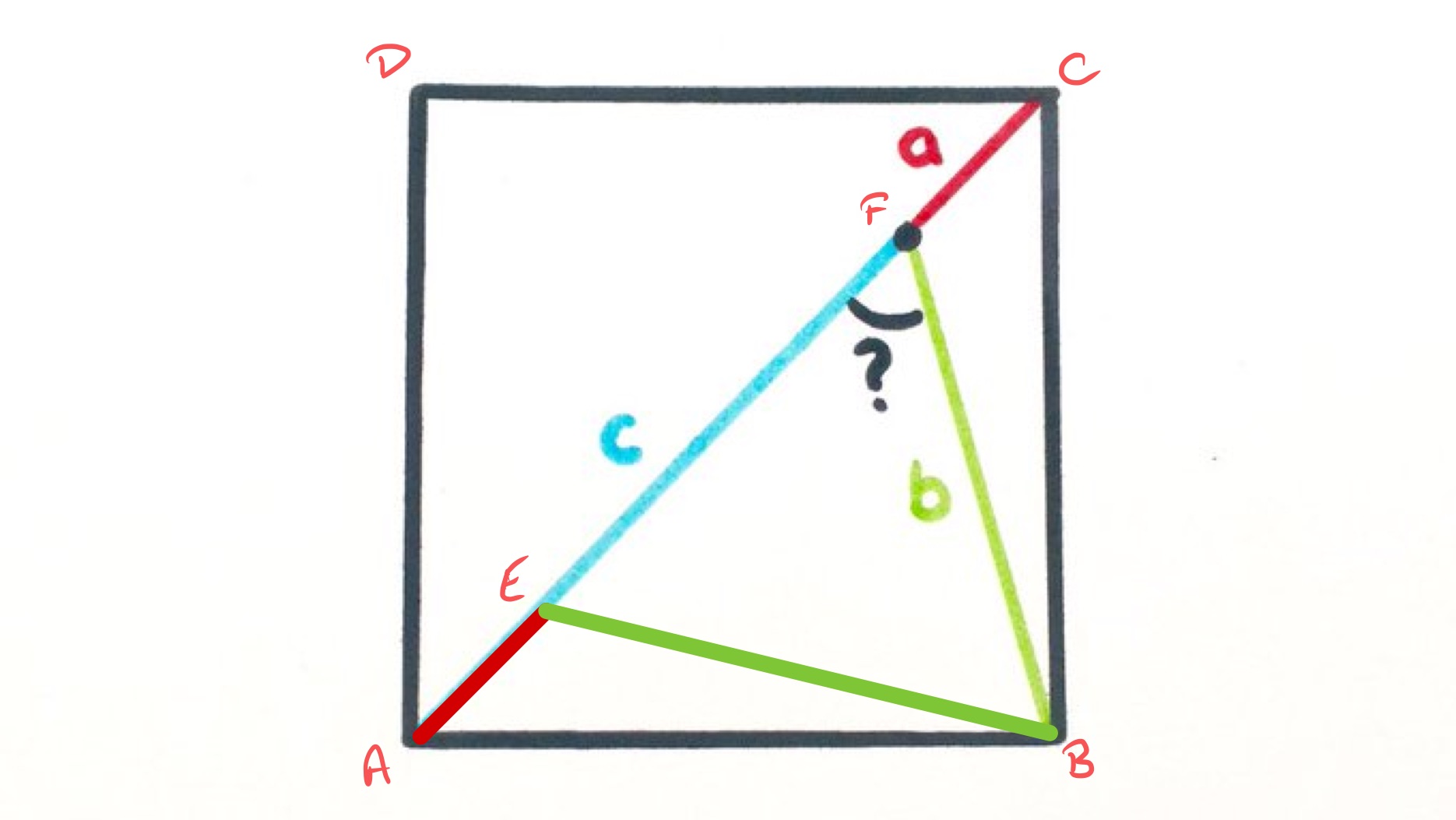
In the diagram above, is on the diagonal so that is the same length as , namely . The length of is then which, from the statement of the problem, is . By symmetry, is also of length so is an equilateral triangle and angle is .