Notes
concentric semi-circles solution
Concentric Semi-Circles
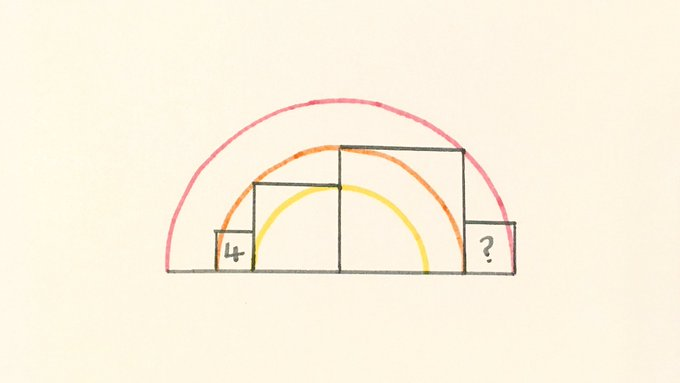
The leftmost square has area . What’s the area of the square on the right?
Solution by Lengths in a Square
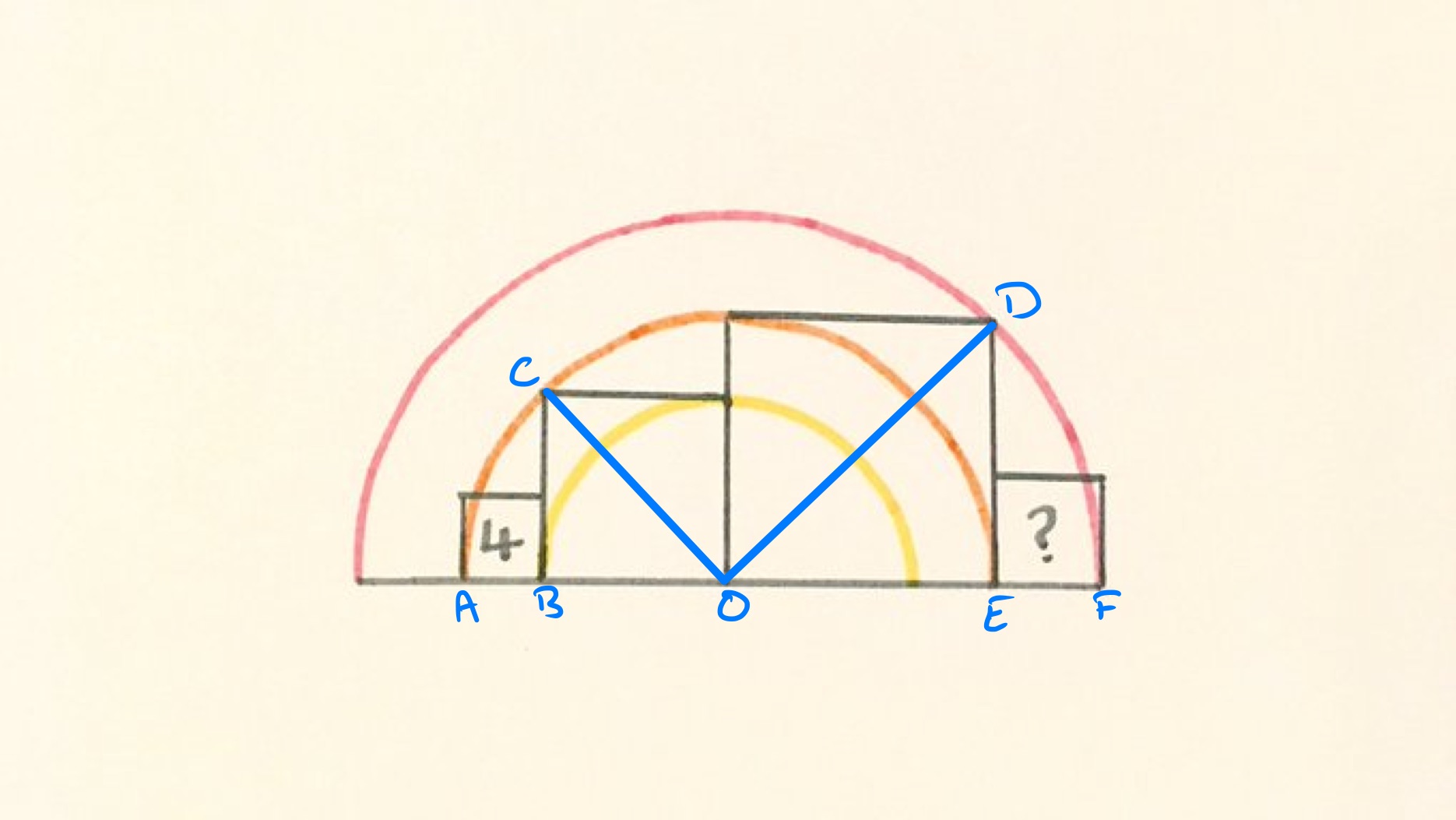
Let the radii of the three circles be , , and in increasing order, so has length , has length , and has length . Since is also a radius of the middle circle, also has length but it also has length . So .
Then is the diagonal of a square with side length , so using the relationship between lengths in a square, . Putting this together with the above, so . Then .
Since is the diagonal of a square with side length , . Then has length which is . The square therefore has area .
Solution by Similarity
In the above diagram, the half of the diagram on the right is similar to the half of the diagram on the left. The scale factor is since is the same length as and this is times the length of . Therefore, the area scale factor is and so the square with side has double the area of that with side , hence has area >