Notes
circles resting on triangles solution
Circles Resting on Triangles
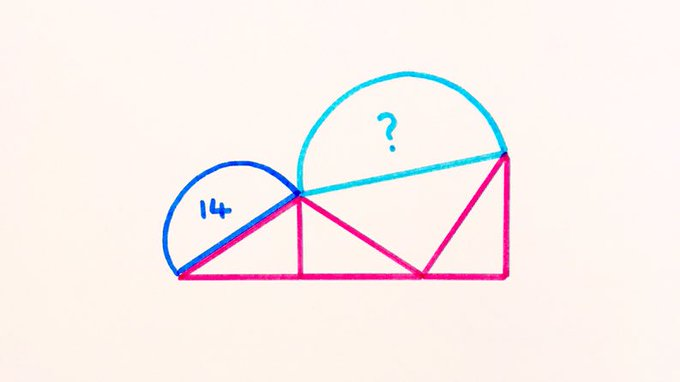
Two semicircles are balanced on these three identical triangles. What’s the missing area?
Solution by Lengths in an Isosceles Right-Angled Triangle, Angles in a Triangle, and Angles at a Point on a Straight Line
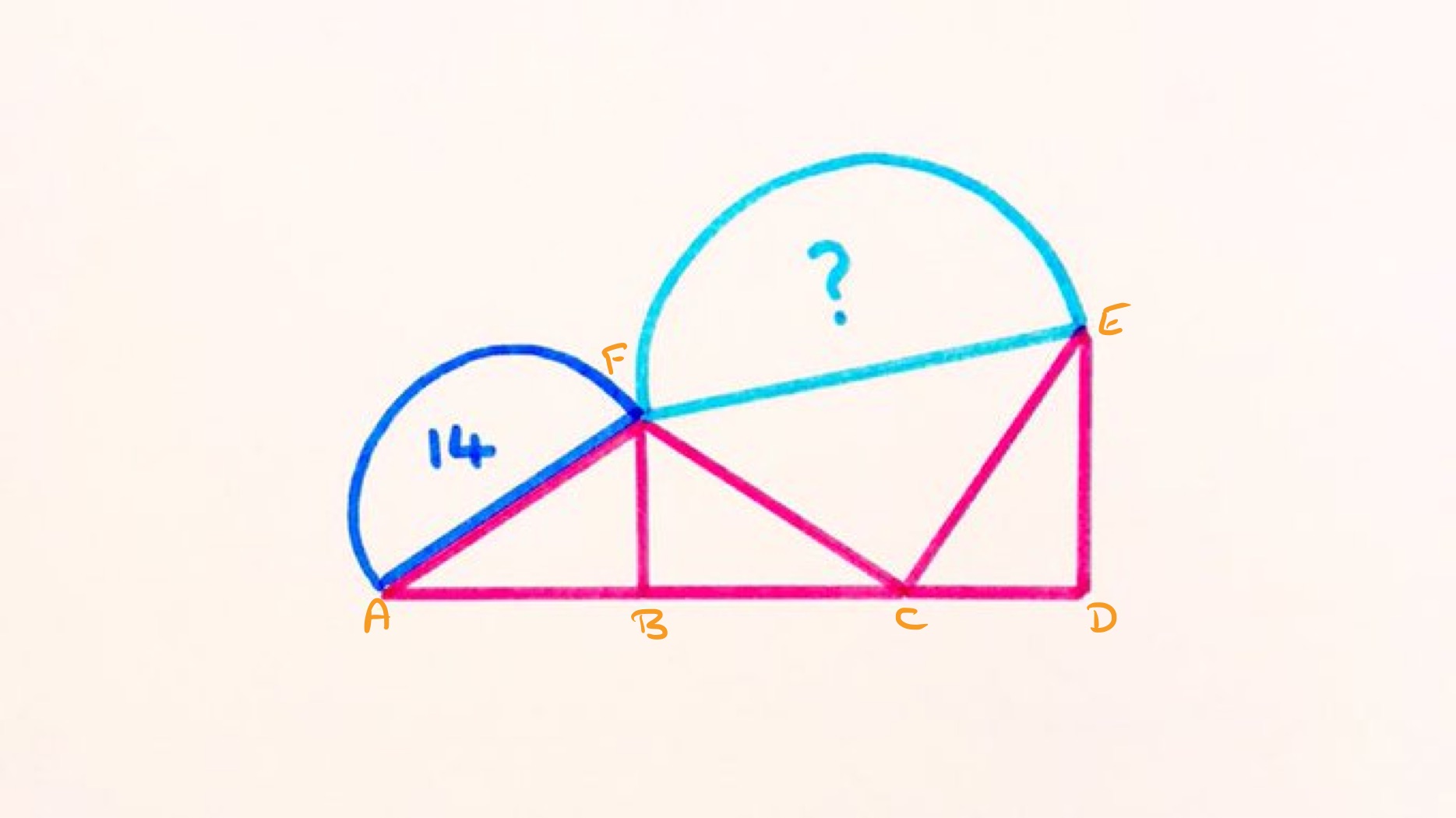
The triangles are identical and is a straight line, so angles and are the same and add to , hence both are right-angles. Then angles and are equal to the non-right-angles, so since the angles in a triangle add up to , these must add up to . This leaves for angle . Since and are the same length, triangle is therefore an isosceles right-angled triangle. The length of is then times that of and so the length scale factor from the dark blue semi-circle to the cyan one is . The area scale factor is thus and so the area of the cyan semi-circle is .