Notes
circles in rhombii sequel solution
Solution to the Circles in Rhombii Sequel Puzzle
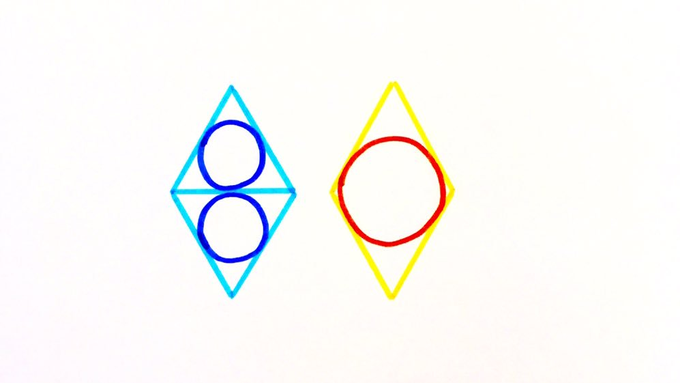
A follow up question: hopefully by now you can convince yourself that the red circle covers a greater proportion of the rhombus than the two blue circles. So can you construct a different rhombus where these proportions would be equal?
Solution by Trigonometry
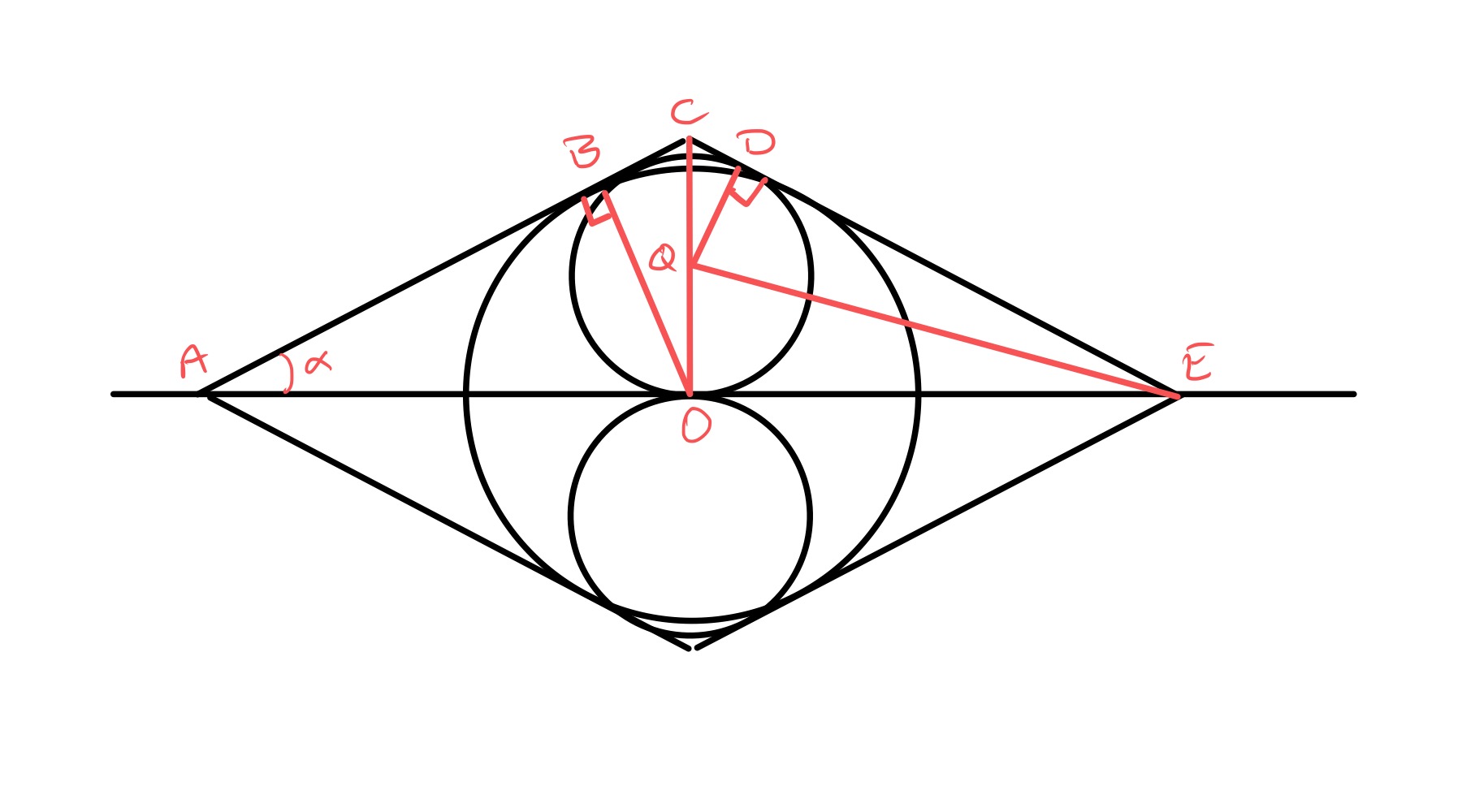
Consider a rhombus as in the diagram above with as angle . For simplicities’ sake, set the length as unit. Then is the hypotenuse of the right-angled triangle so the length of is .
The point labelled is the centre of the upper small circle. The point labelled is where the circle touches the line , so and are radii of this circle and so of equal length. Therefore, triangles and are congruent, so angles and are equal and therefore both equal to . Since has length , this means that has length .
The goal is for the large circle to have the same length as the two smaller circles combined, so the area of the large circle is double that of one of the smaller circles, and so the radius of the larger circle is times that of the smaller. This implies:
The half-angle formulae show that with then . Substituting in to the above gives:
which rearranges to and so (taking the positive square root as is acute).
This gives a value of as to significant figures.