Notes
circles in overlapping triangles solution
Solution to the Circles in Overlapping Triangles Puzzle
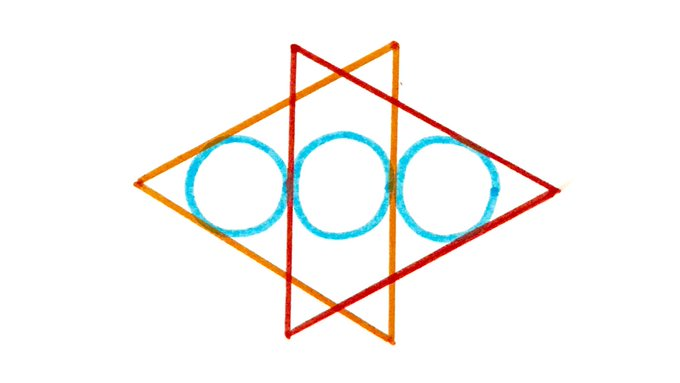
Two overlapping equilateral triangles each have an area of . The three circles are the same size. What’s the total area of the design?
Solution by Lengths in an Equilateral Triangle and Area Scale Factor
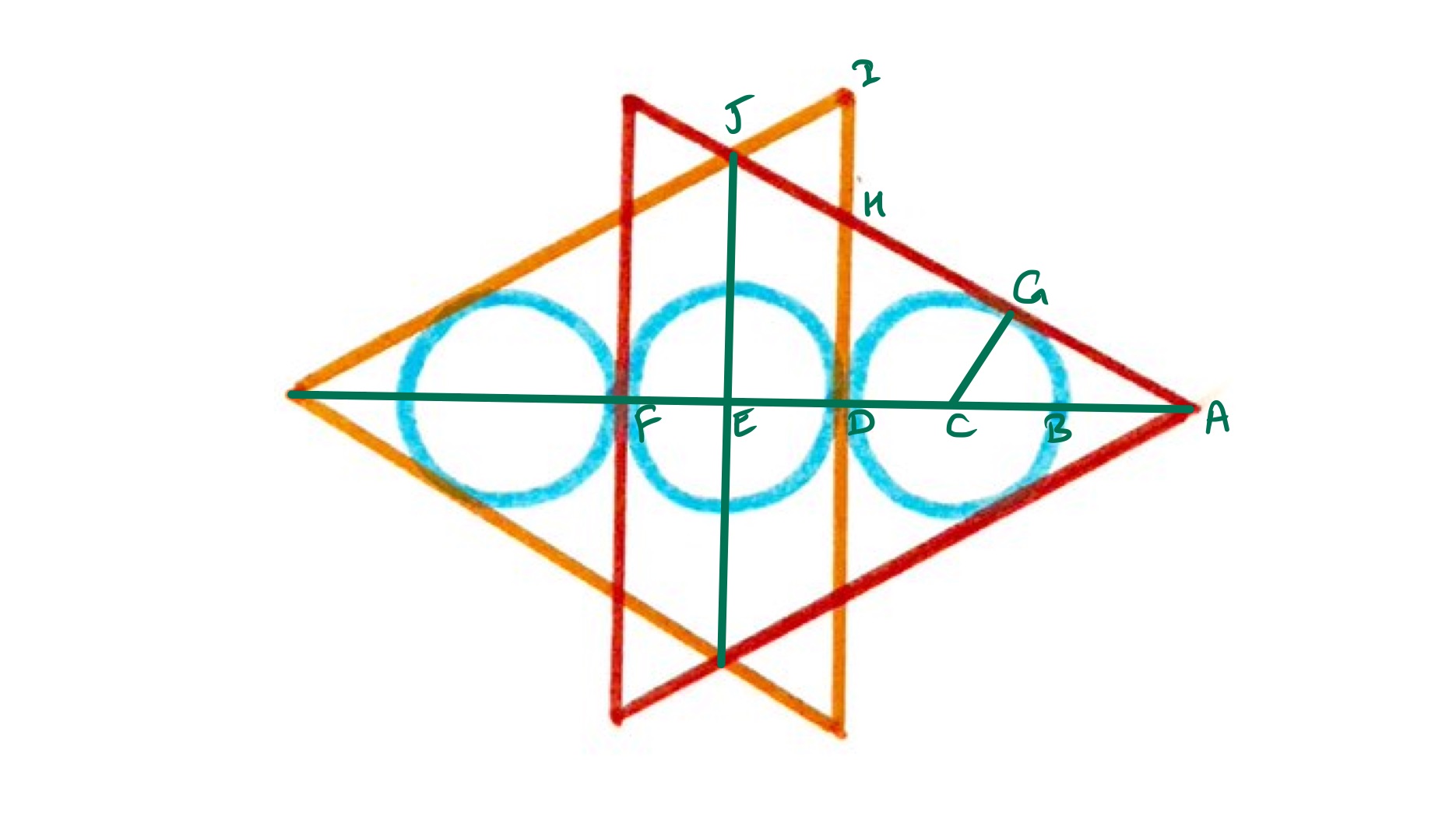
In the above diagram, the points labelled and are the centres of their circles, while is such that angle is a right-angle.
The line that extends cuts the red triangle in half, so angle is which shows that triangle is half an equilateral triangle. This means that the length of is twice that of , so the length of is the same as the radius of the circles. The length of is therefore of these lengths, and is of them.
Cutting the red equilateral triangle at gives a triangle ths of the height of the red one, which therefore has area ths of the red as the area scale factor is the square of the length scale factor. Since the red triangle has area , this shorter triangle has area .
Triangle is also equilateral and its height (of above ) is one radius of the blue circles, which is one fifth of the red triangle. Its area is therefore one twenty-fifth of the area of the red triangle, which is .
The total area of the design is therefore: