Notes
circle inside a triangle solution
Solution to the Circle Inside a Triangle Puzzle
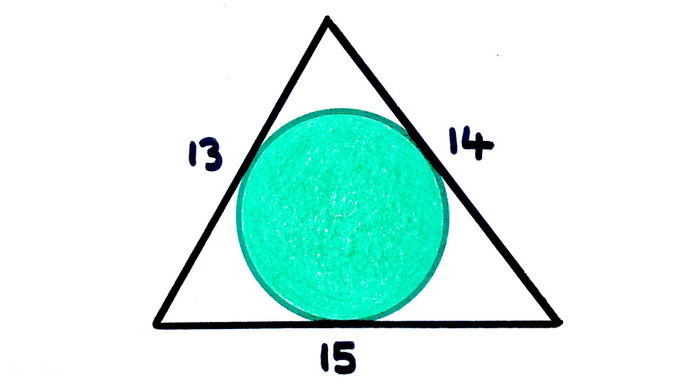
What’s the area of the circle?
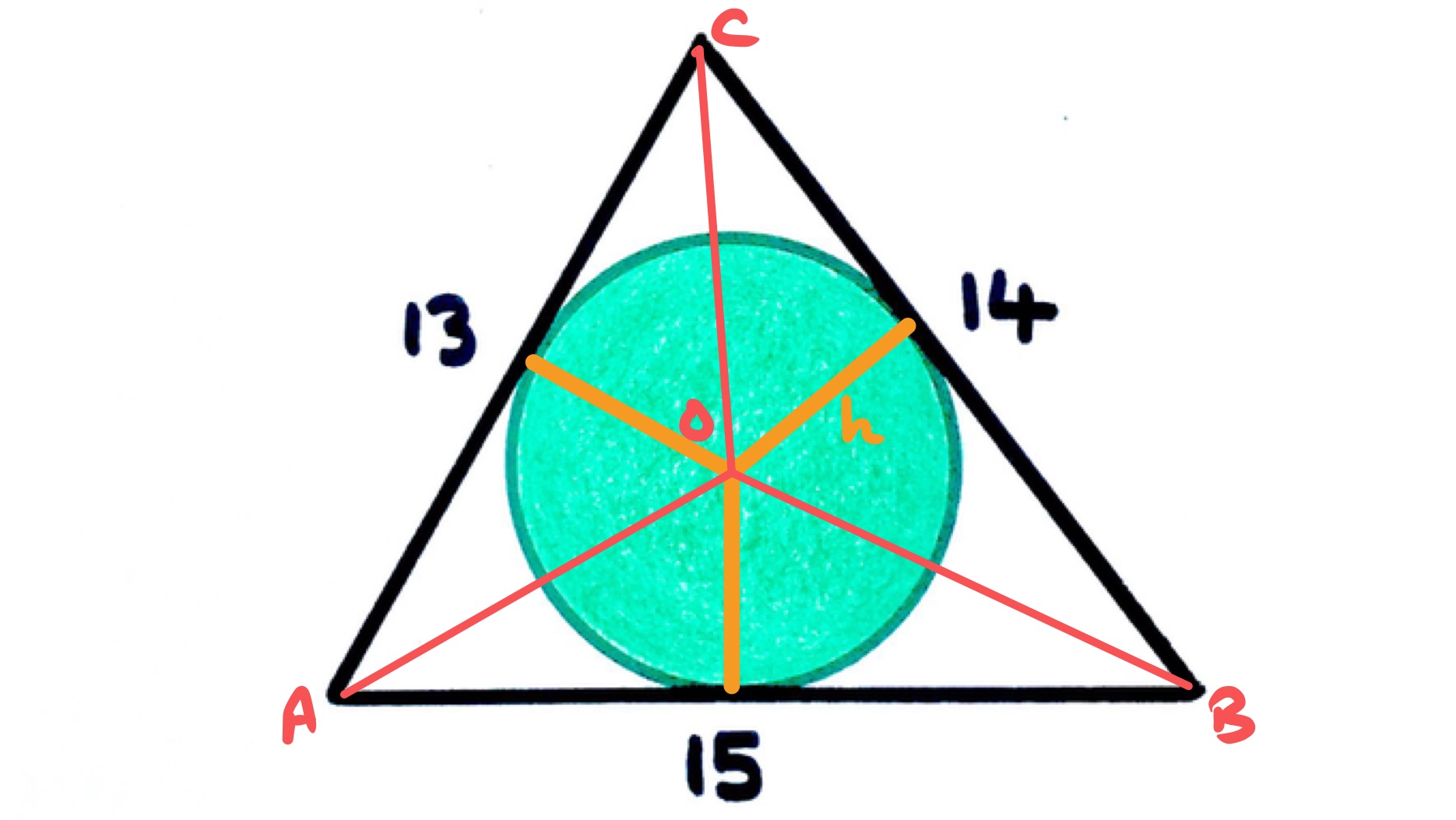
Decomposing the triangle as above shows that its area can be written as:
The area can be established either using Heron's formula or Pythagoras' theorem.
Using Heron's formula, the area is written in terms of the semi-perimeter which is .
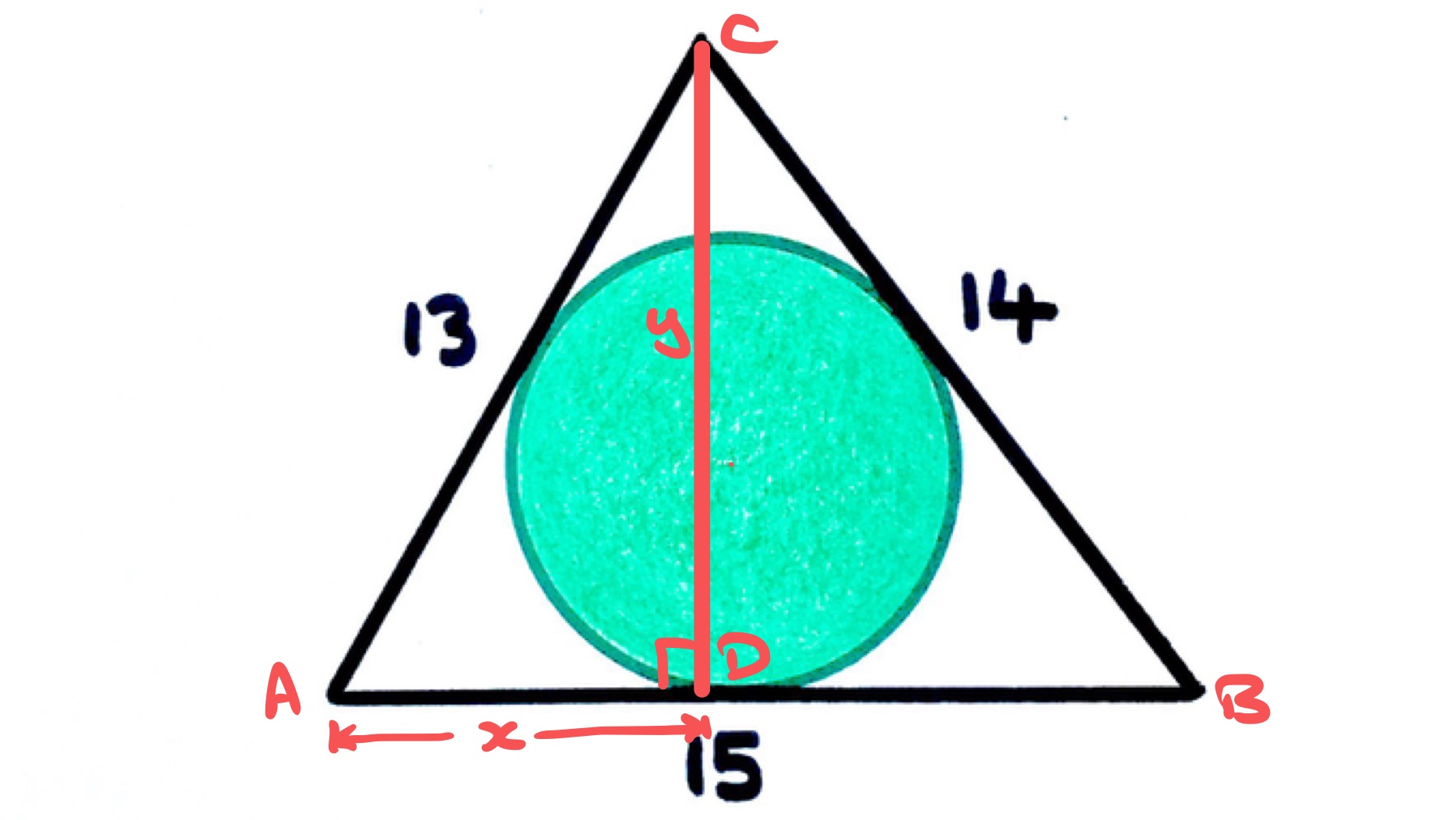
To use Pythagoras' theorem, mark a point directly below on the edge so that forms a right-angled triangle.
Applying Pythagoras' theorem to the two right-angled triangles and yields:
So and . The area of the triangle is therefore
Created on July 8, 2021 10:33:37
by
Andrew Stacey