Notes
circle in triangle in square solution
Solution to the Circle in Triangle in Square Puzzle
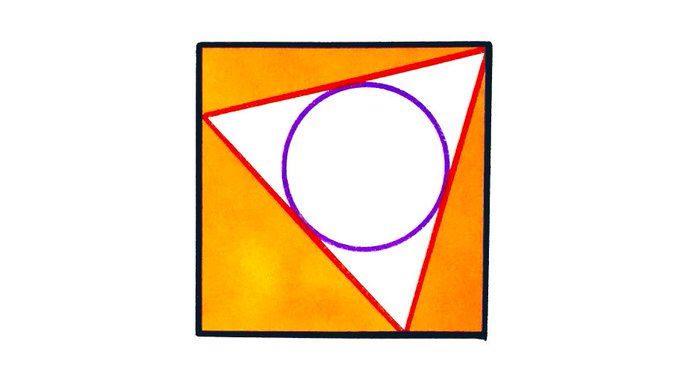
A unit circle sits in an equilateral triangle inside a square. What’s the total shaded area?
Solution by Properties of Equilateral Triangles
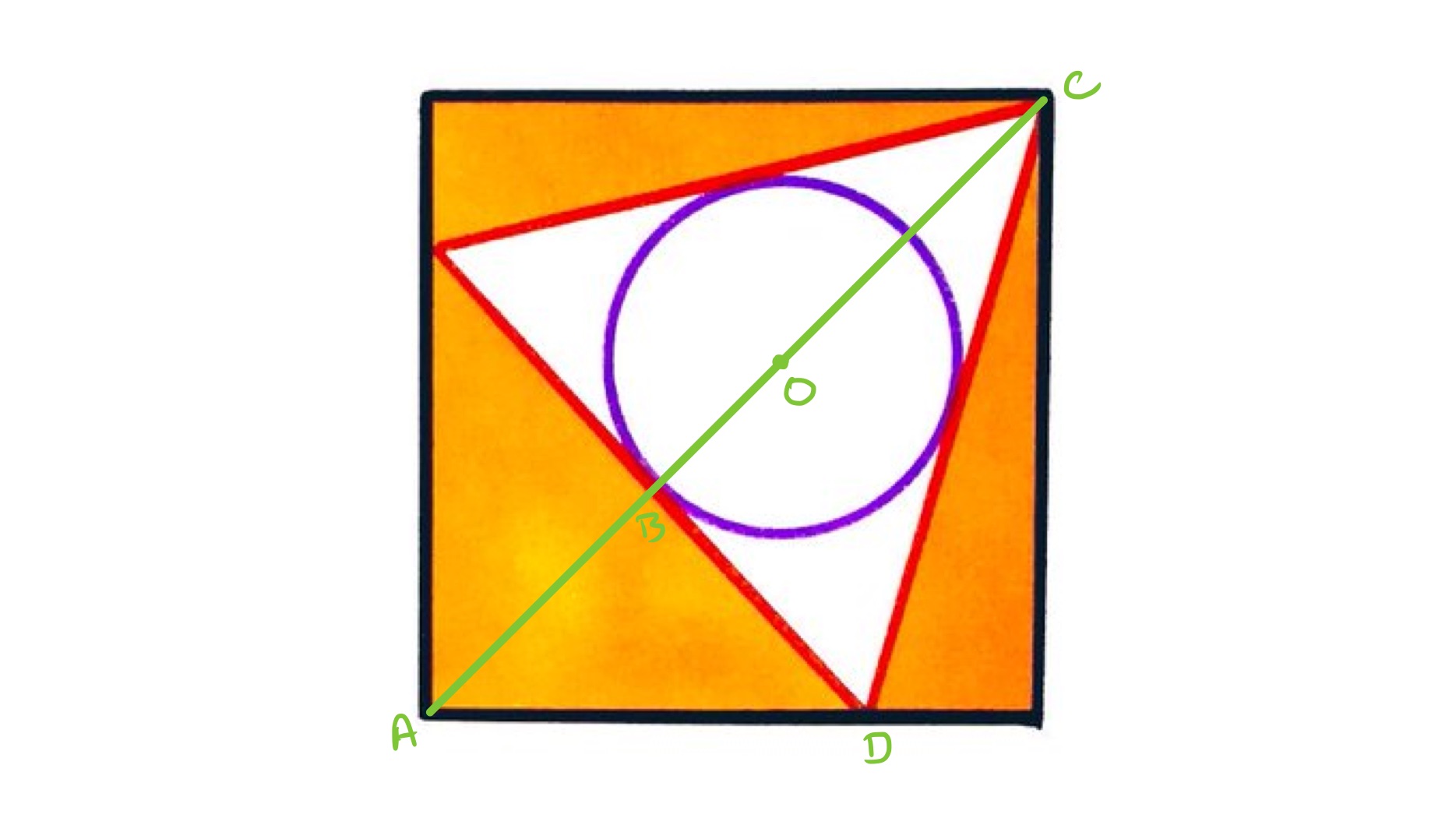
From lengths in an equilateral triangle, the length of is one third of , so has length . Then the length of is times the length of , so has length . Triangle is isosceles and right-angled, so has the same length as . The length of the diagonal of the square is then . The area of the square is .
Since the area of an equilateral triangle is times the square of the length of one of its sides, the triangle has area . The shaded area is therefore .