Notes
circle in a quarter circle solution
Circle in a Quarter Circle
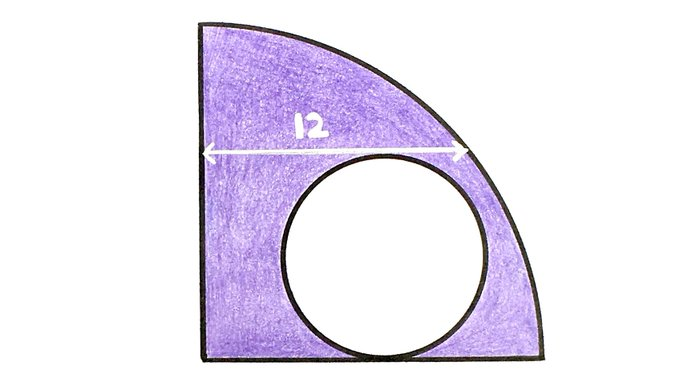
What’s the total shaded area?
Solution by Pythagoras' Theorem and Area of a Circle
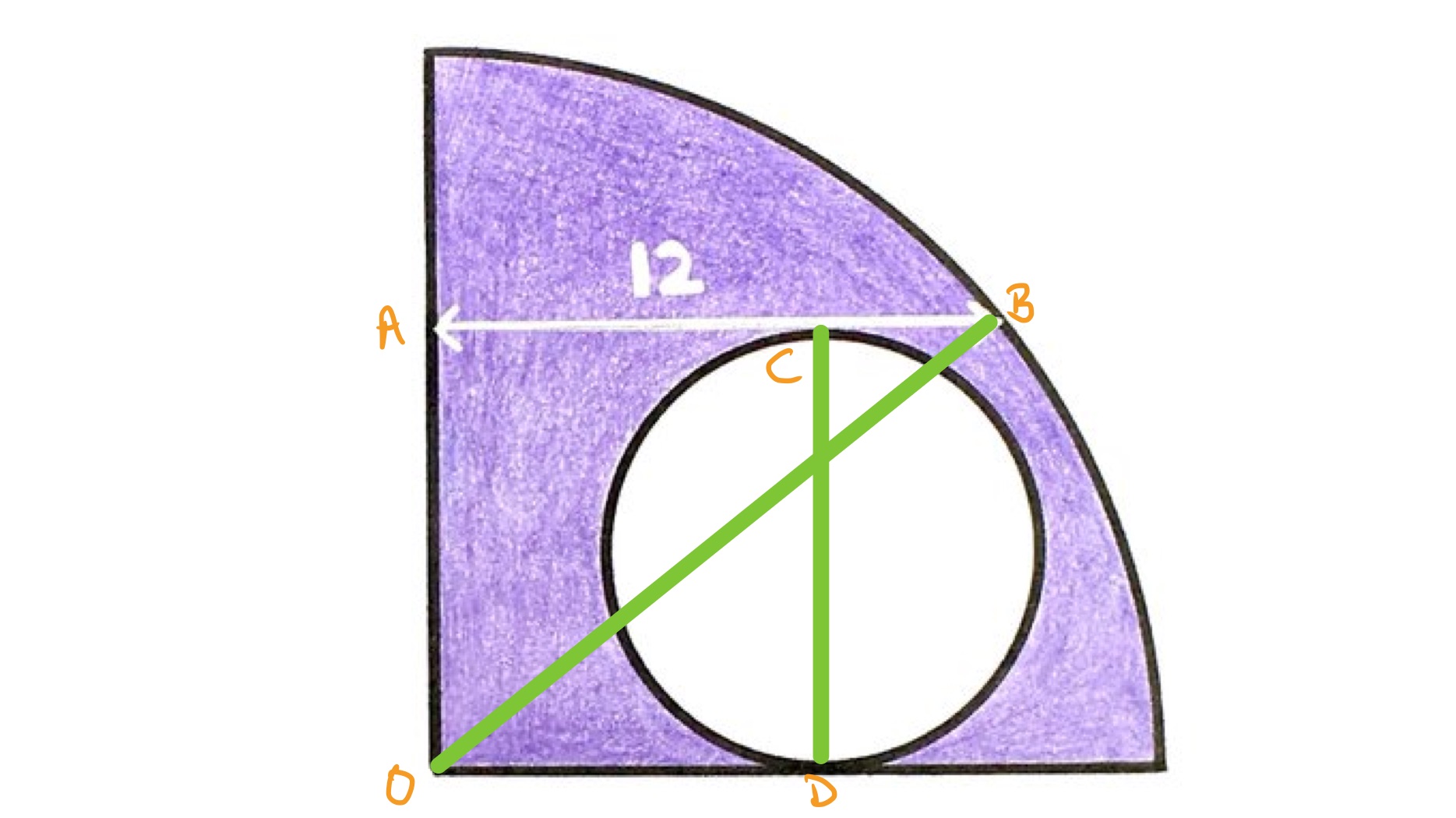
Let be the radius of the quarter circle, which is the length of , and let be the radius of the smaller circle, so the length of is . The lengths of and are the same, so applying Pythagoras' theorem to right-angled triangle shows that:
The area of the quarter circle is and the area of the inner circle is , so the area of the shaded region is:
So the area of the shaded region is .