Notes
circle and semi-circle in triangle solution
Solution to the Circle and Semi-Circle in Triangle Puzzle
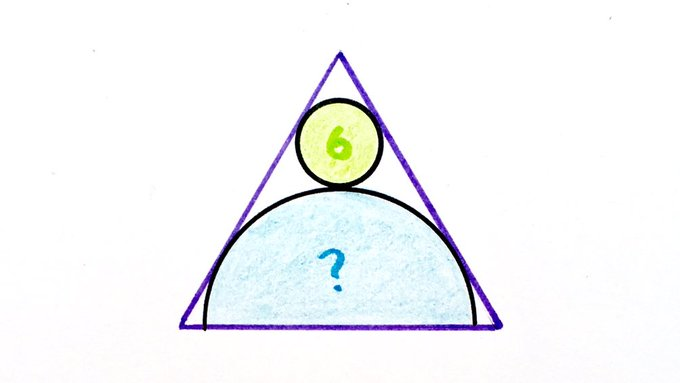
What’s the area of the semicircle inside this equilateral triangle?
Solution by Lengths in an Equilateral Triangle and Area Scale Factor
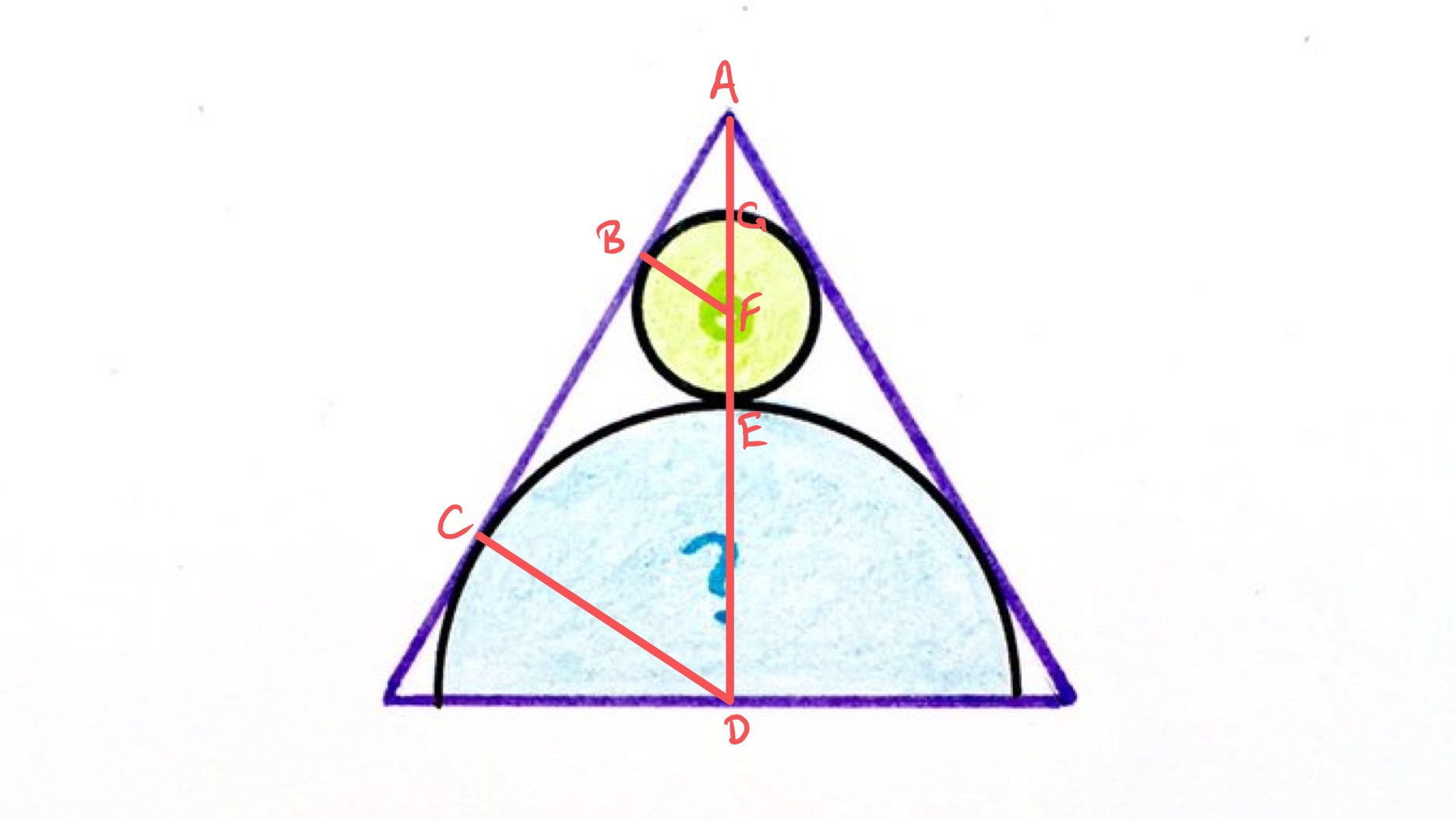
In the above diagram, the points and are such that and are both perpendicular to . As the line cuts the equilateral triangle in half, angle is , so triangle is half an equilateral triangle. Similarly, so is triangle . This means that the length of is twice that of and the length of of twice that of . So the length of is three times the radius of the small circle and is the same length as the radius of the large semi-circle. The area scale factor is then , so the large semi-circle has area .