Notes
chord splitting a square in half solution
Solution to the Chord Splitting a Square in Half Puzzle
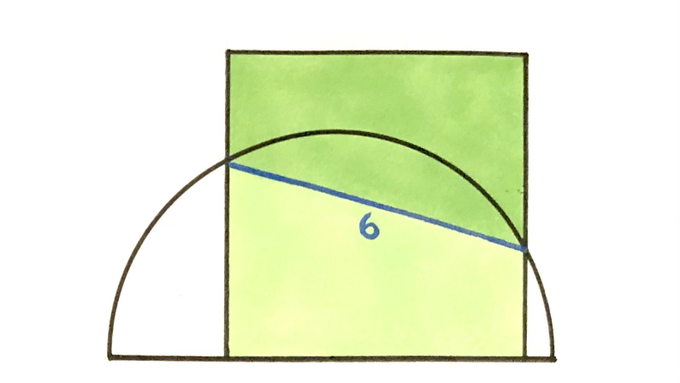
A chord, of length , splits the square in half. What’s the area of the semicircle?
Solution by Symmetry and lengths in an isosceles right-angled triangle
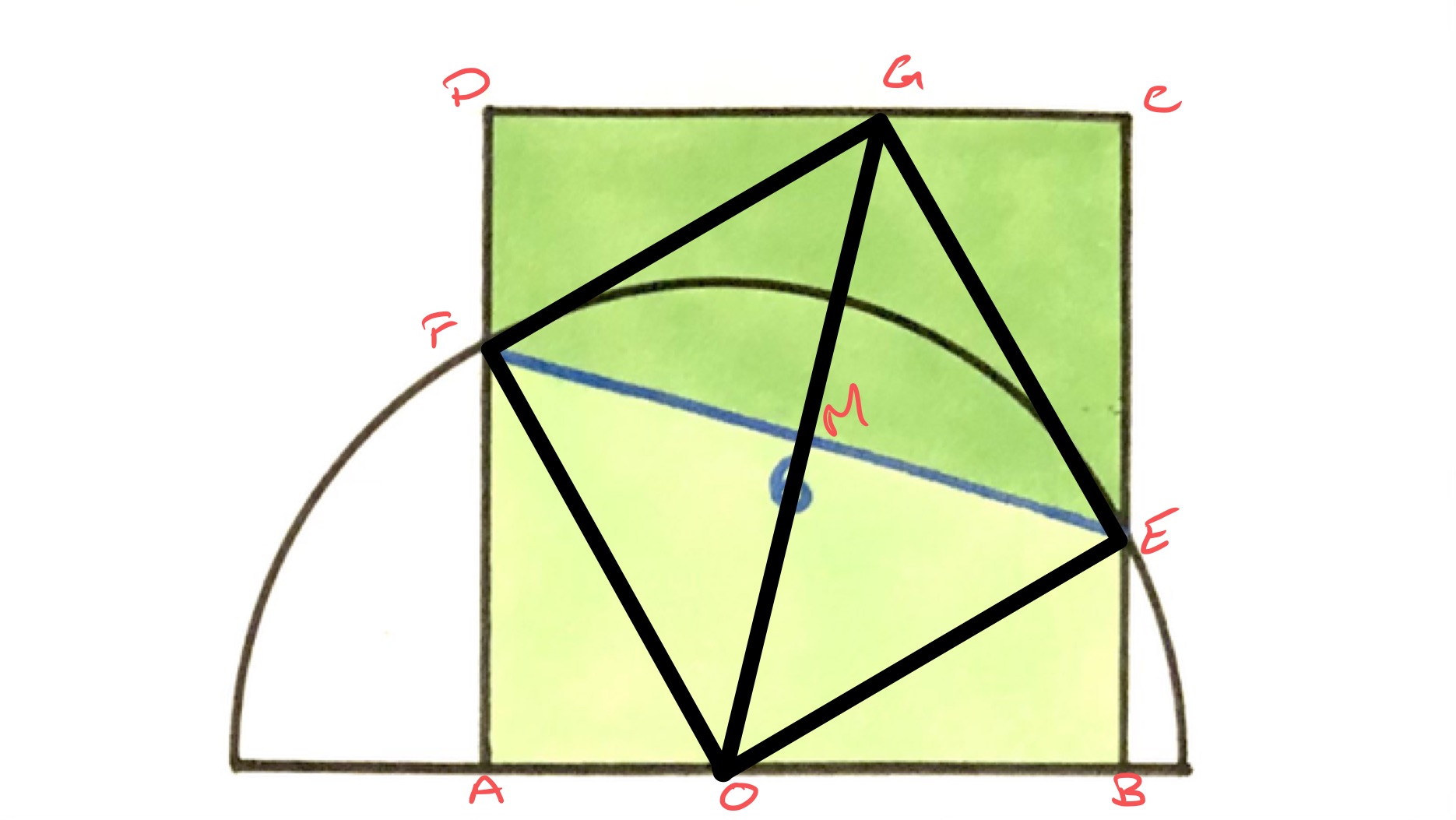
In the above diagram, point is the centre of the semi-circle, so and are radii. Point is the midpoint of the chord , so the line is perpendicular to . Point is where the line extending meets .
As the line segment splits the square in half, point is also the middle of the square. So rotating the square anticlockwise about rotates exactly onto . This shows that is itself a square, and so angle is a right-angle. Hence triangle is an isosceles right-angled triangle and so is in length.
The area of the semi-circle is then .
Solution by Invariance principle
The chord can be drawn at any angle. Two possibilities make the radius of the semi-circle straightforward to deduce.
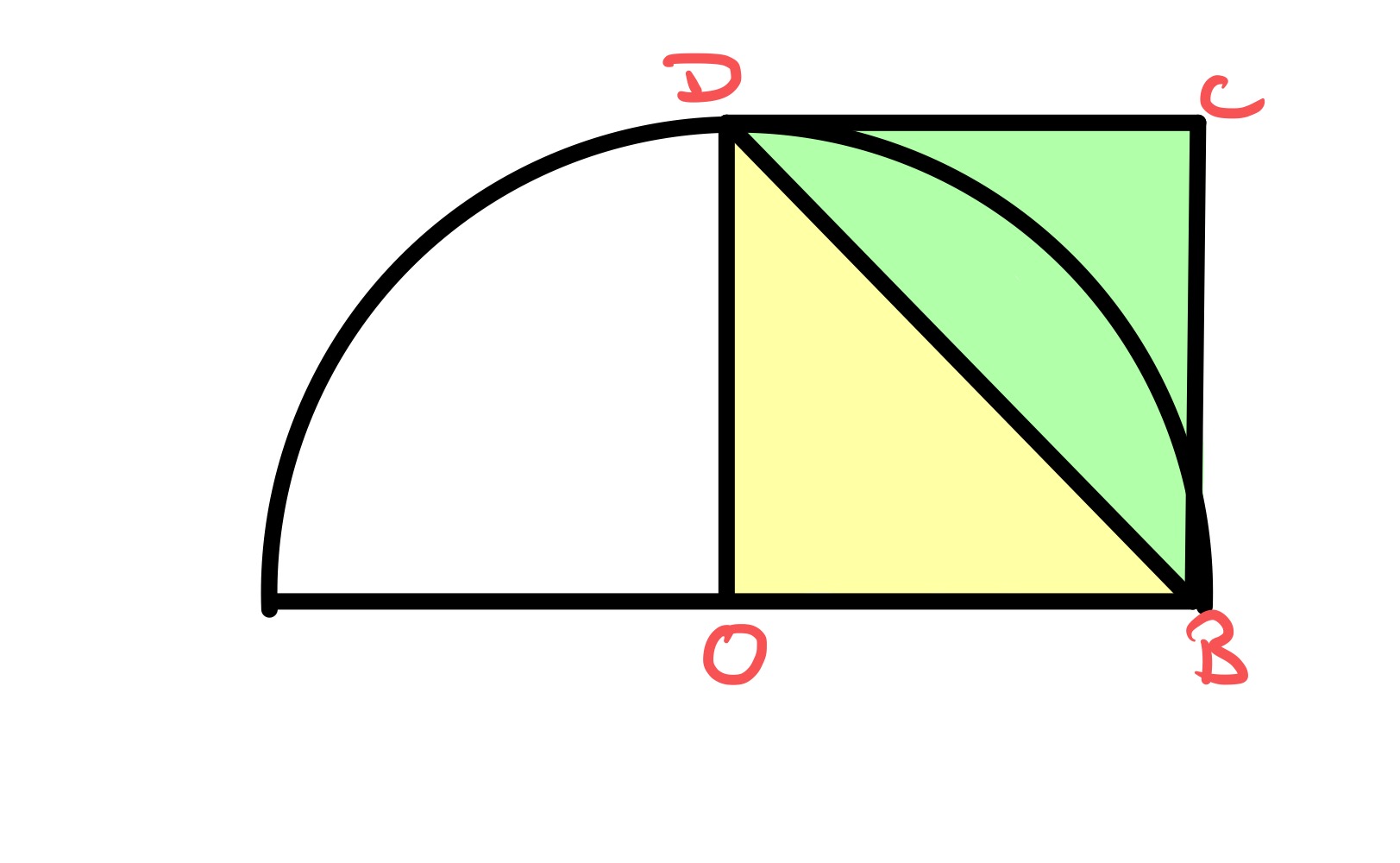
In this case, the point coincides with and so to split the square in half the chord must be a diagonal of the square and the sides and are radii of the semi-circle.
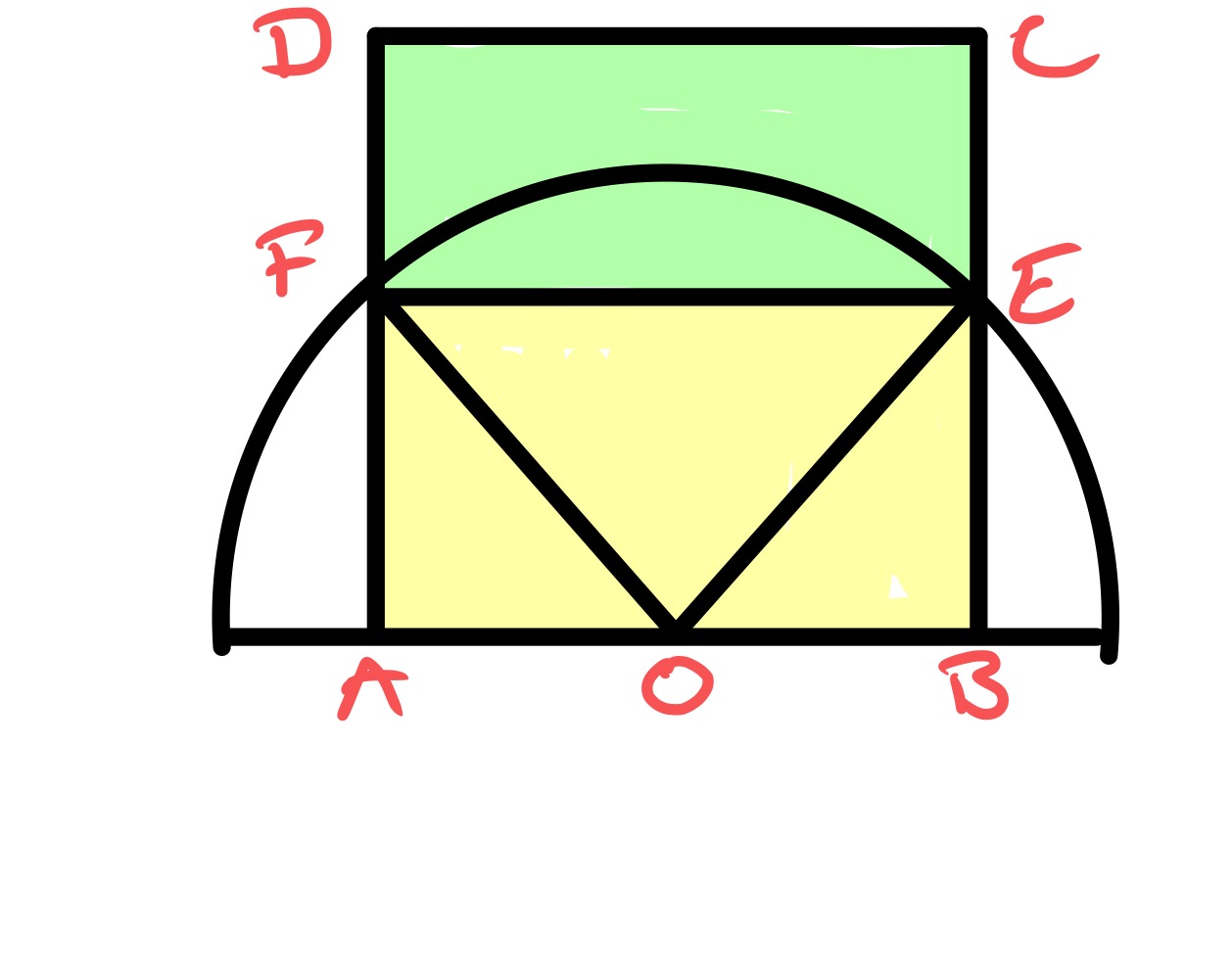
In this case, the chord is drawn horizontally. The isosceles right-angled triangle has hypotenuse a radius and other sides of length , establishing the radius as .