Notes
arcs inside a triangle solution

Arcs Inside a Triangle

Solution by Lengths in an Equilateral Triangle and Pythagoras' Theorem

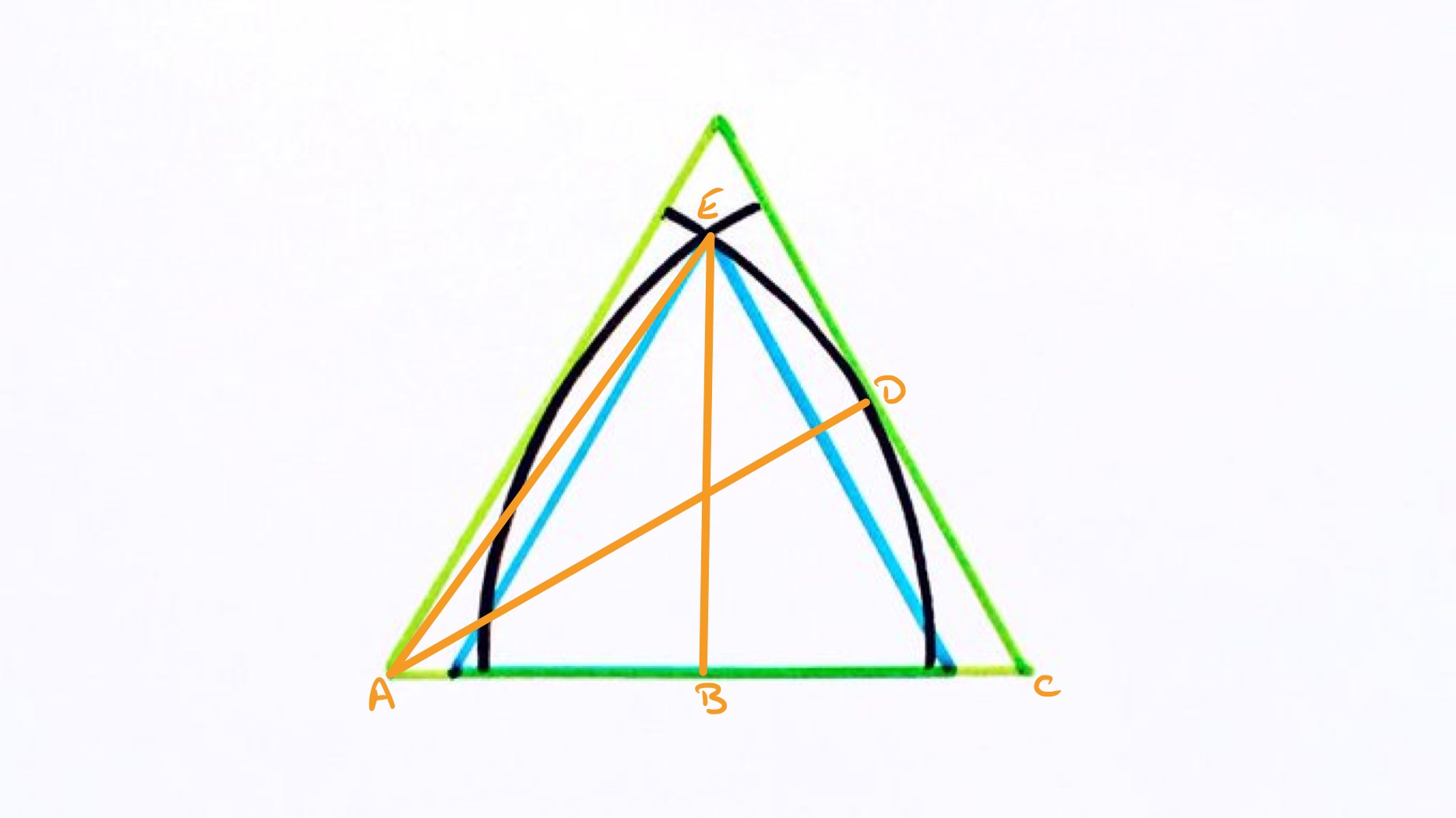
Let $x$ and $y$ be the side lengths of the green and blue triangles, respectively. Using the relationships between the lengths in an equilateral triangle, the height of the green triangle is $\frac{\sqrt{3}}{2} x$. As the right-hand edge of the green triangle is tangent to the arc centred at $A$, angle $A \hat{D} C$ is the angle between a radius and tangent so is $90^\circ$. This establishes $D$ as the midpoint of that side and so the length of $A D$ is $\frac{\sqrt{3}}{2} x$. Then $A E$ has the same length.

The point marked $B$ is the midpoint of $A C$, making $A B E$ a right-angled triangle. The length of $E B$ is the height of the green equilateral triangle, so is $\frac{\sqrt{3}}{2} y$. The length of $A B$ is $\frac{1}{2} x$. Applying Pythagoras' theorem then shows that:

The area scale factor from the green to the blue triangles is therefore $\frac{2}{3}$. Since the green triangle has area $3$, the blue triangle has area $2$.