Notes
arcs in a semi-circle solution
Arcs in a Semi-Circle
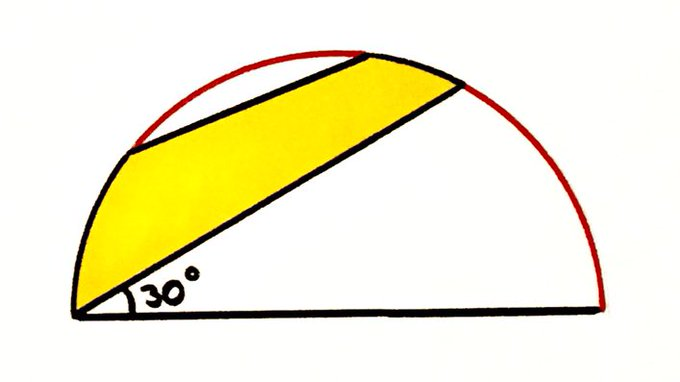
The two red arcs are the same length. What fraction of the semicircle is shaded?
Solution by Angle at the Centre is Twice the Angle at the Circumference and Area of a Triangle
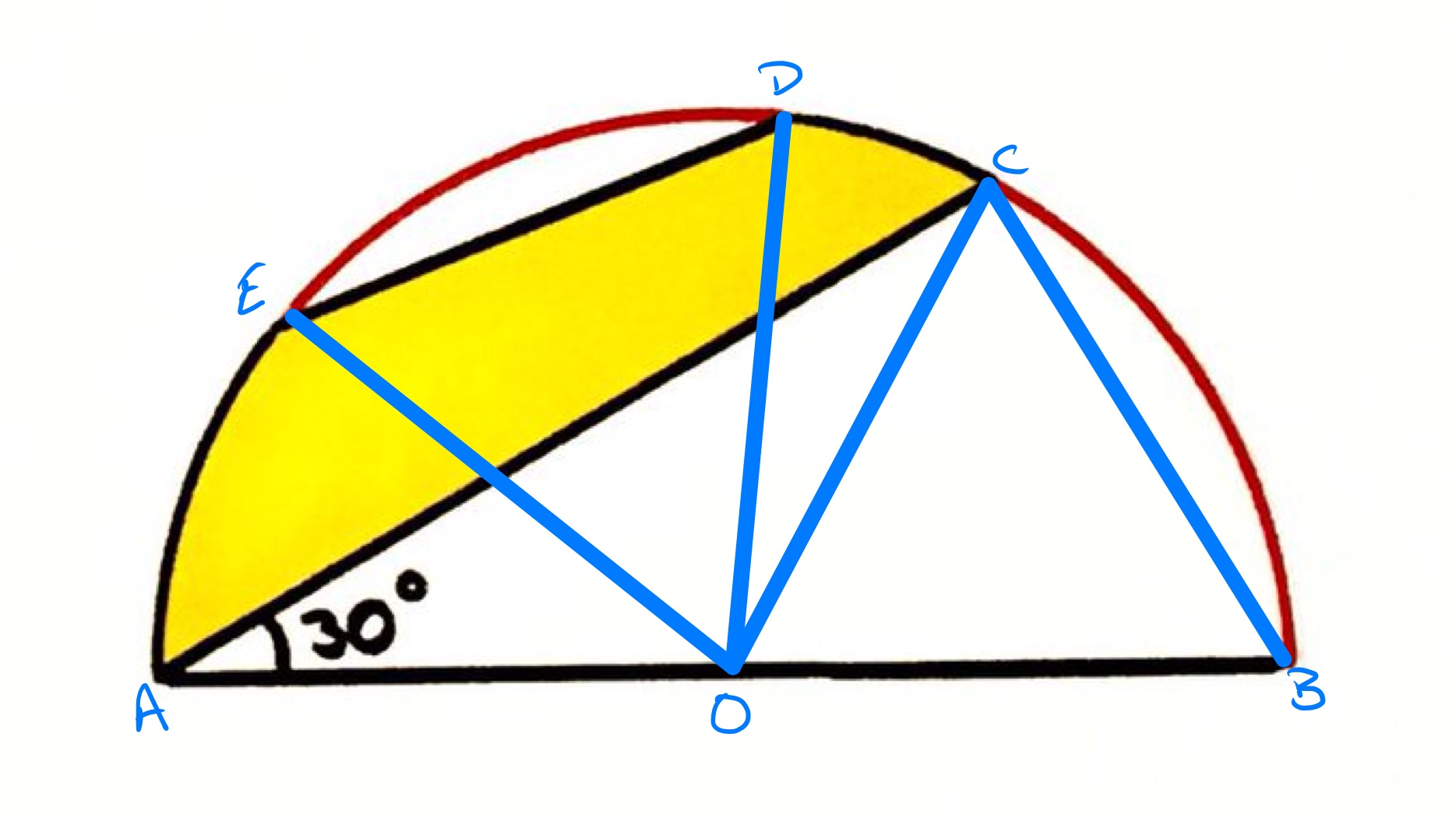
In the above diagram, the point labelled is the centre of the semi-circle.
Since the angle at the centre is twice the angle at the circumference, angle is . The red arcs have the same length, so angle is also . The region between the arc and the chord is congruent to that defined by and . The triangles and both have the same base, as it is a radius of the circle, and height, as their height is the height of above the base, so have the same area. Therefore, the combined area of triangle with the region defined by and is the same as the sector . So the unshaded region has the same area as two sectors with central angle . Therefore the shaded region has the same area as one such sector and so consists of rd of the semi-circle.