Notes
arbelos solution
Arbelos
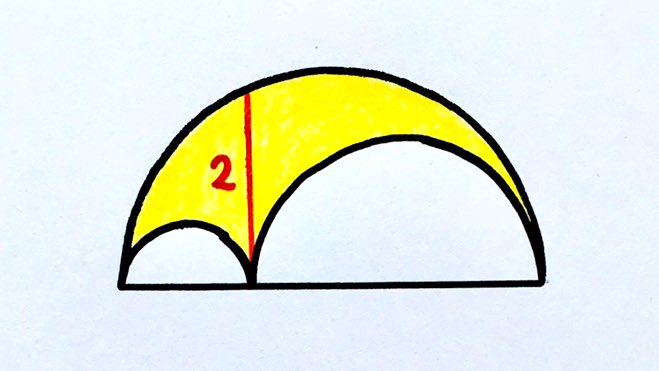
The red line, of length , is perpendicular to the bases of the three semicircles. What’s the total shaded area?
Solution by Angle in a Semi-Circle and Pythagoras' Theorem
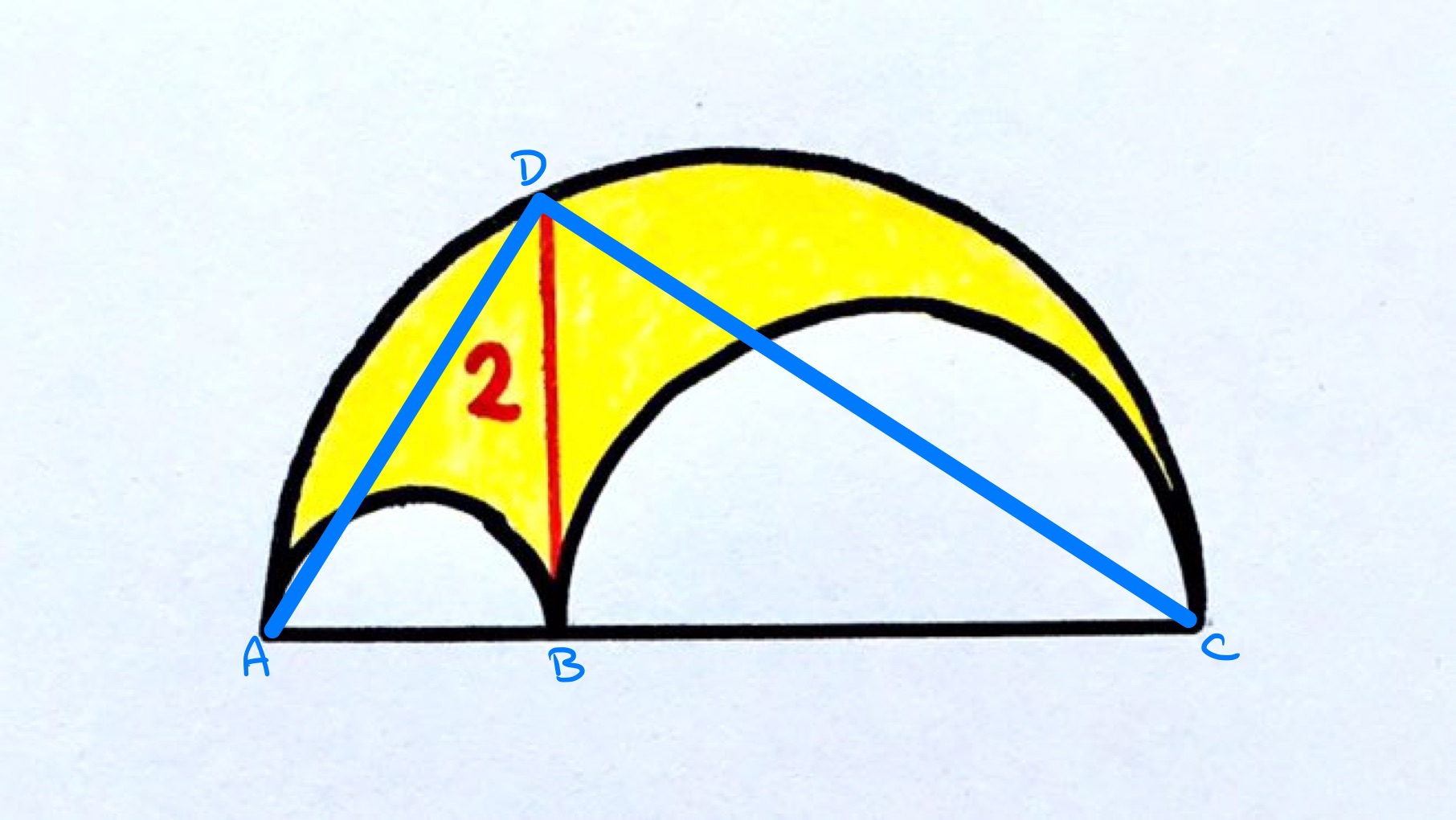
In the above diagram, the angle is a right-angle since it is the angle in a semi-circle. Therefore, triangle is a right-angled triangle.
Let the lengths of , , , , and be , , , , and respectively. Applying Pythagoras' theorem to triangles , , and gives the following identities:
Therefore, . The area of a semi-circle with diameter is , so the area of the shaded region is:
Solution by Intersecting Chords Theorem
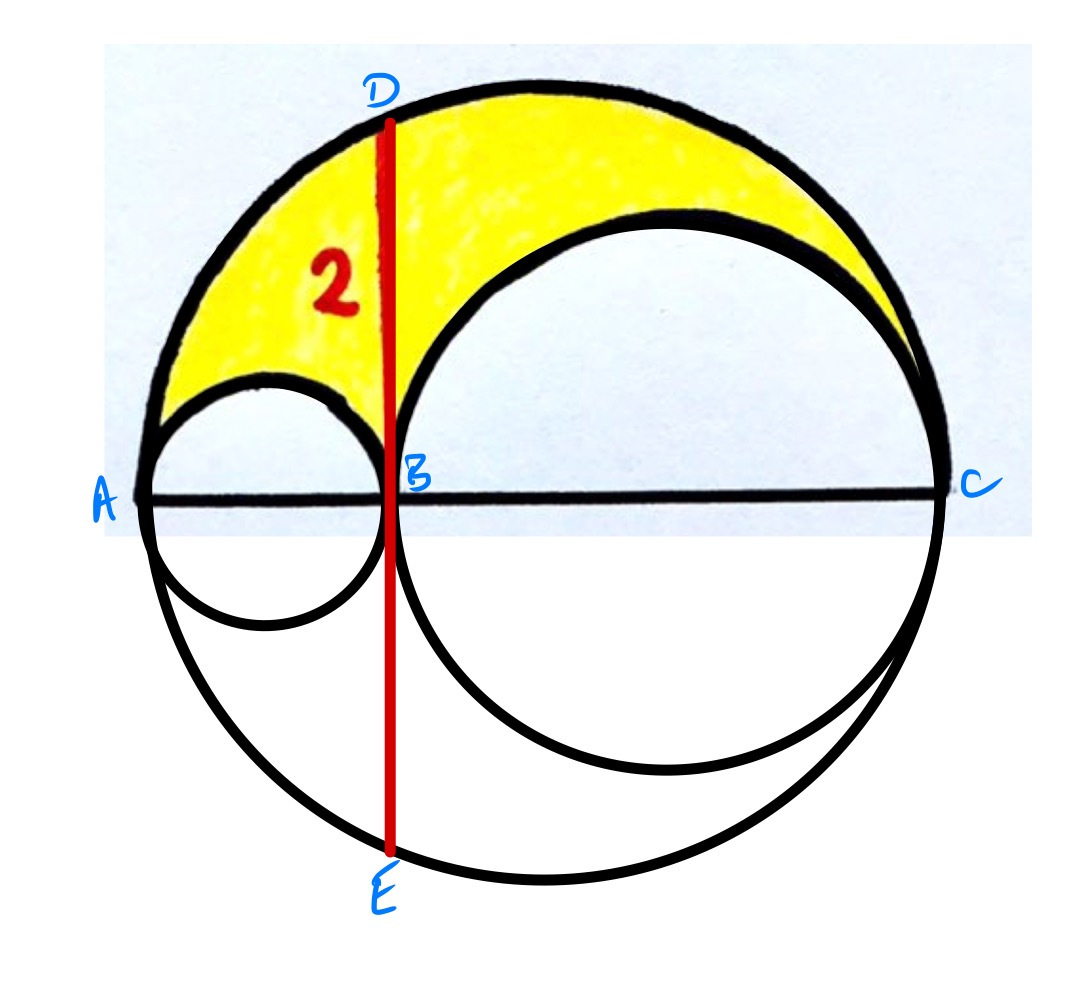
In the above diagram, the original diagram has been reflected in the diameter of the semi-circle. With the distances labelled as before, the intersecting chords theorem shows that . Since , the area of the shaded region is: