Notes
angles in two hexagons solution
Angles in Two Hexagons
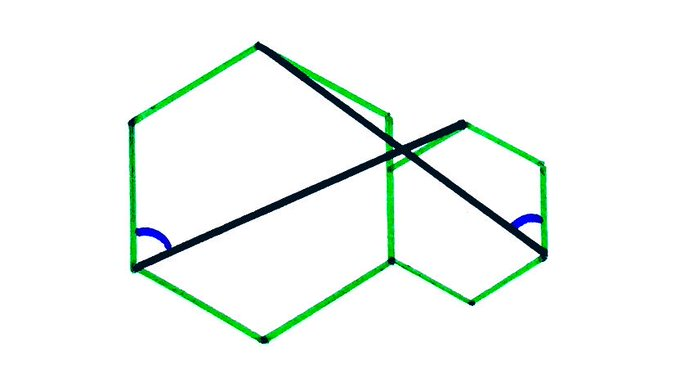
Both hexagons are regular. What’s the sum of these two angles?
Solution by Transformations
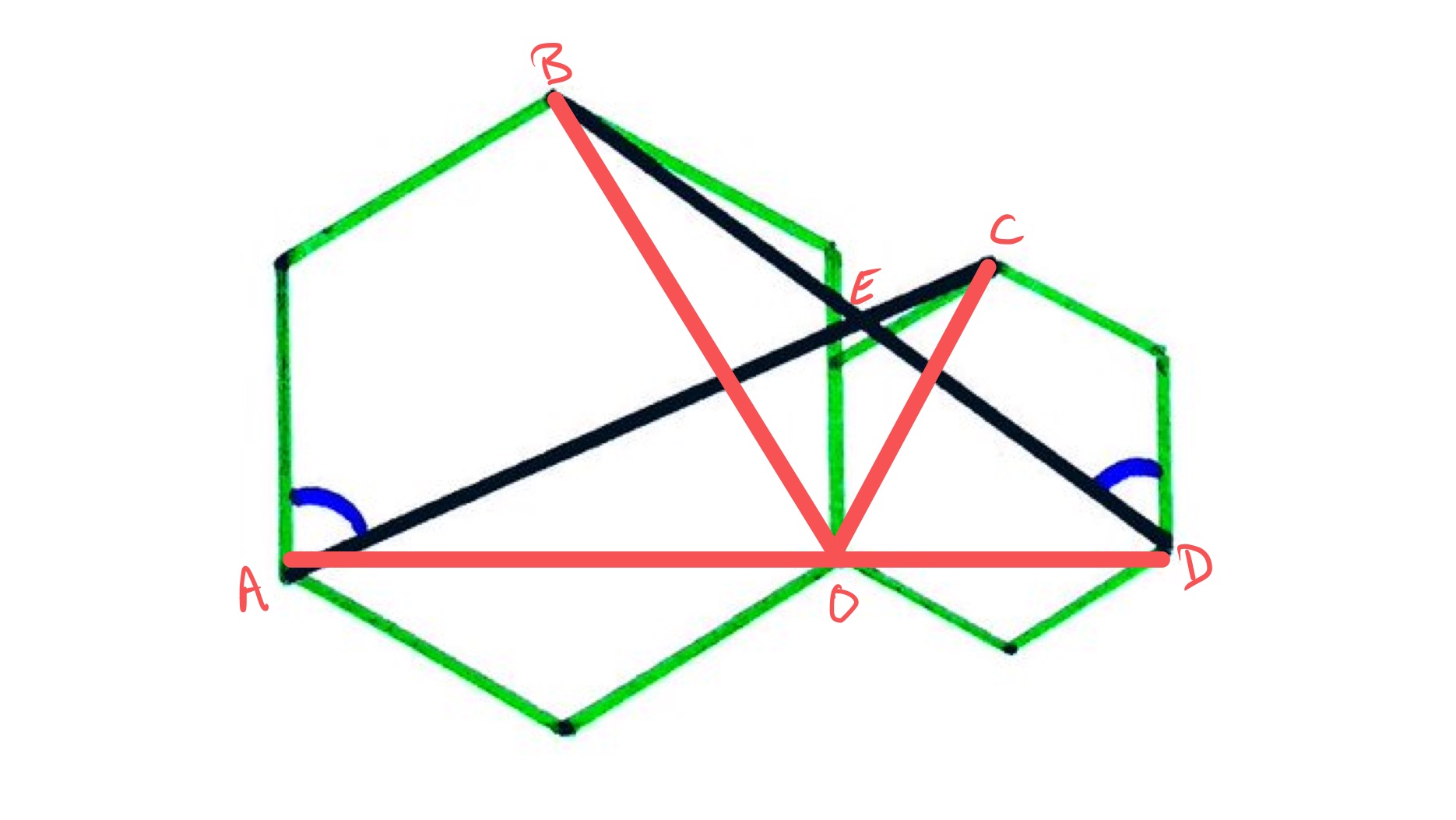
With the points labelled as above, a rotation of clockwise about takes point to point and point to point . It therefore takes the line segment to and so the angle between these line segments is . This is angle , so angle is . Since angles in a triangle add up to , angles and therefore add up to and so the sum of the two marked angles is .
Solution by Invariance Principle
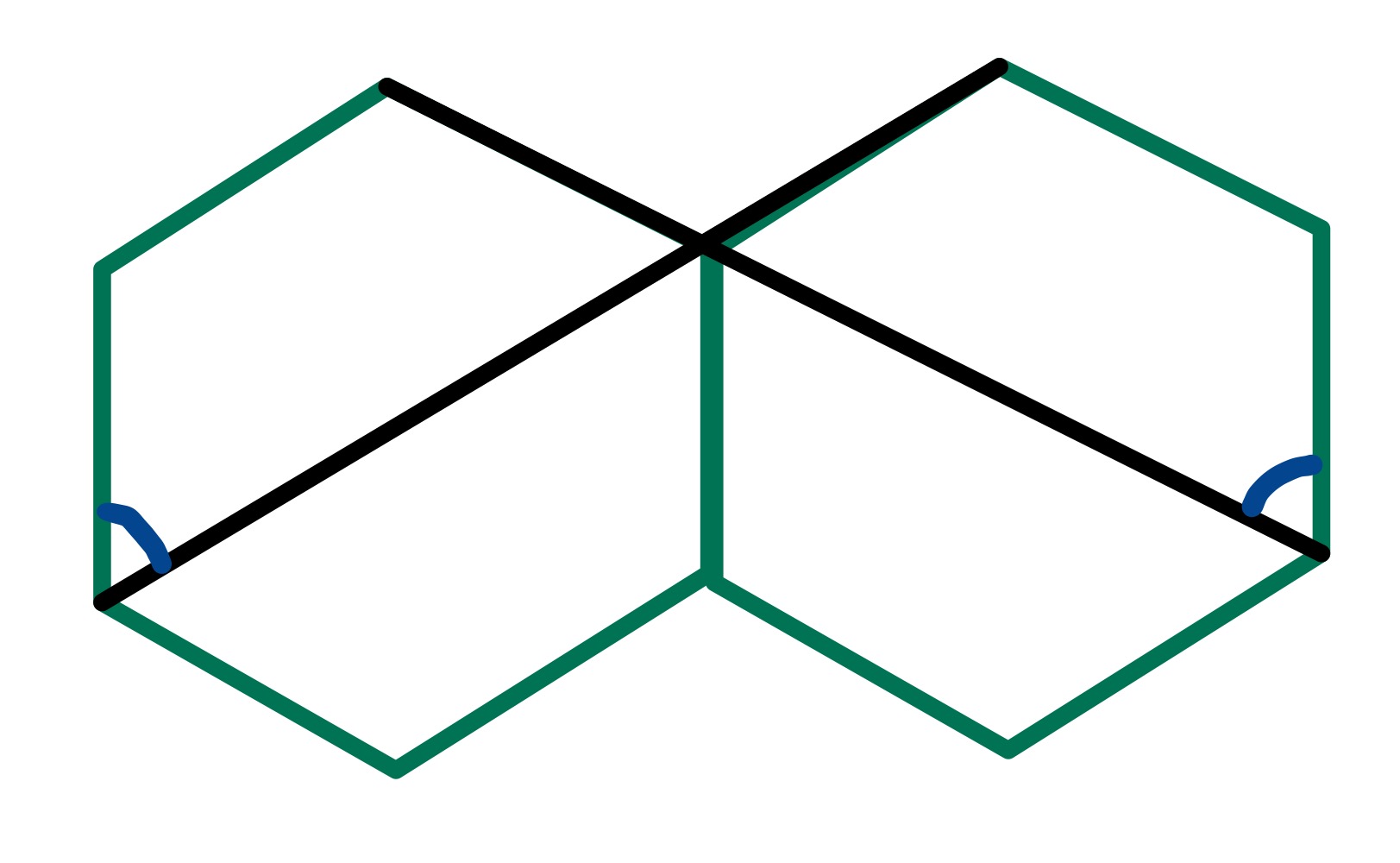
In the case where the two hexagons the same size, the two angles individually are seen to be and their sum is therefore .