Notes
angles in a circle solution
Solution to the Angles in a Circle Puzzle
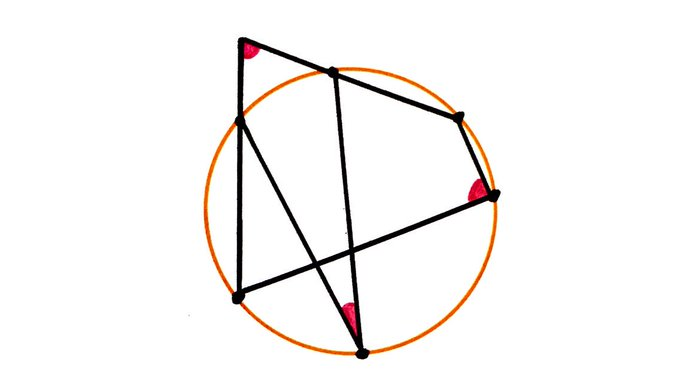
What’s the sum of the three marked angles?
Solution by Angles in the Same Segment, Angles in a Cyclic Quadrilateral, Angles at a Point on a Line, and Angles in a Triangle
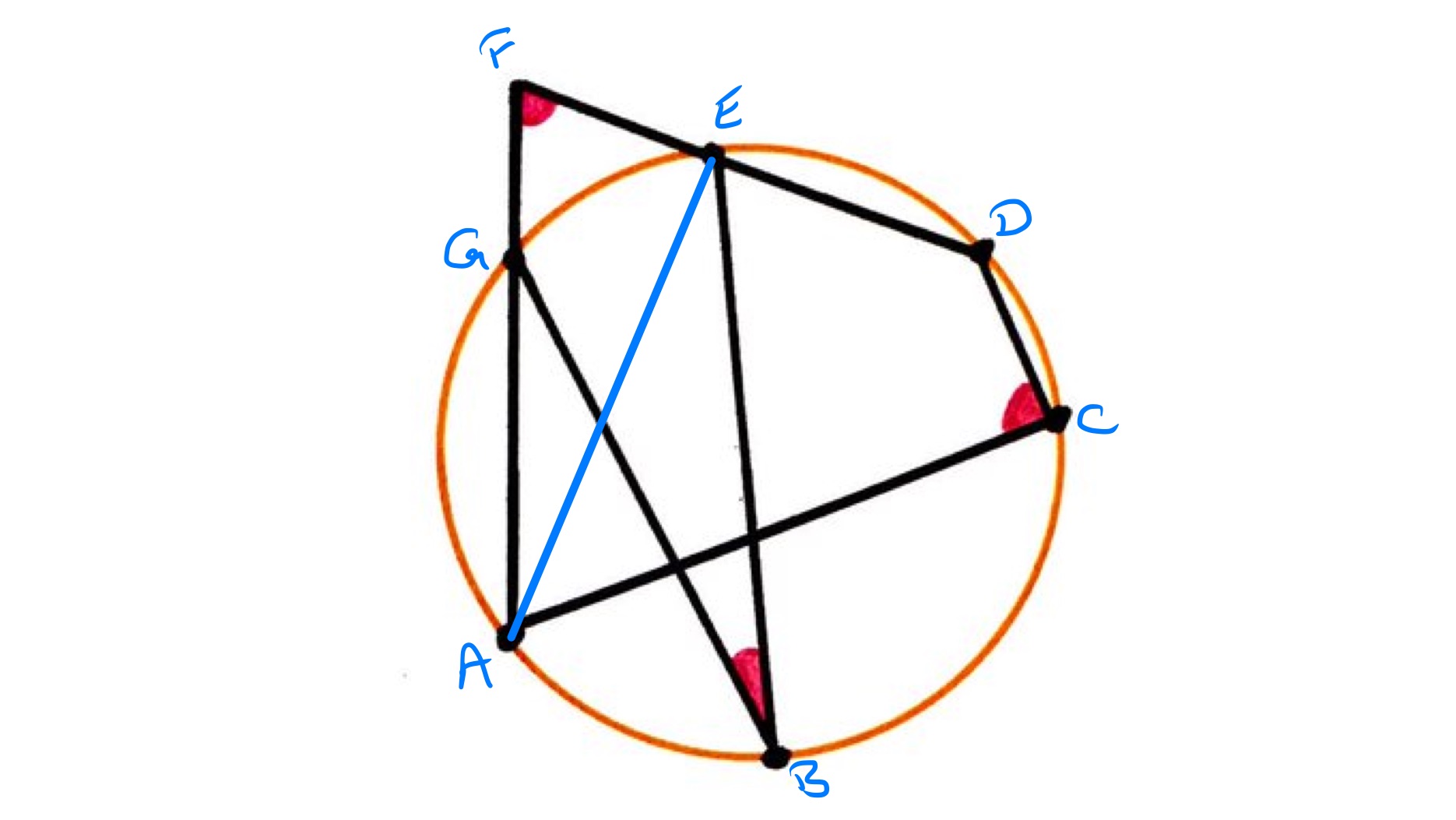
With the points labelled as above, angles and are equal as they are angles in the same segment. Then angles and add up to as they are opposite angles in a cyclic quadrilateral. Angles and add up to since the are angles at a point on a line. Putting these last together shows that angles and are equal. Therefore the three angles in the triangle are each equal to one of the marked angles, so the sum of the three marked angles is as that is the sum of the angles in a triangle.