Notes
angle in a circle and semi-circle solution

Solution to the Angle in a Circle and Semi-Circle Puzzle

Solution by Angles in a Cyclic Quadrilateral, Angle at the Centre is Twice the Angle at the Circumference, Angles in a Triangle, Angles at a Point on a Straight Line, and Vertically Opposite Angles

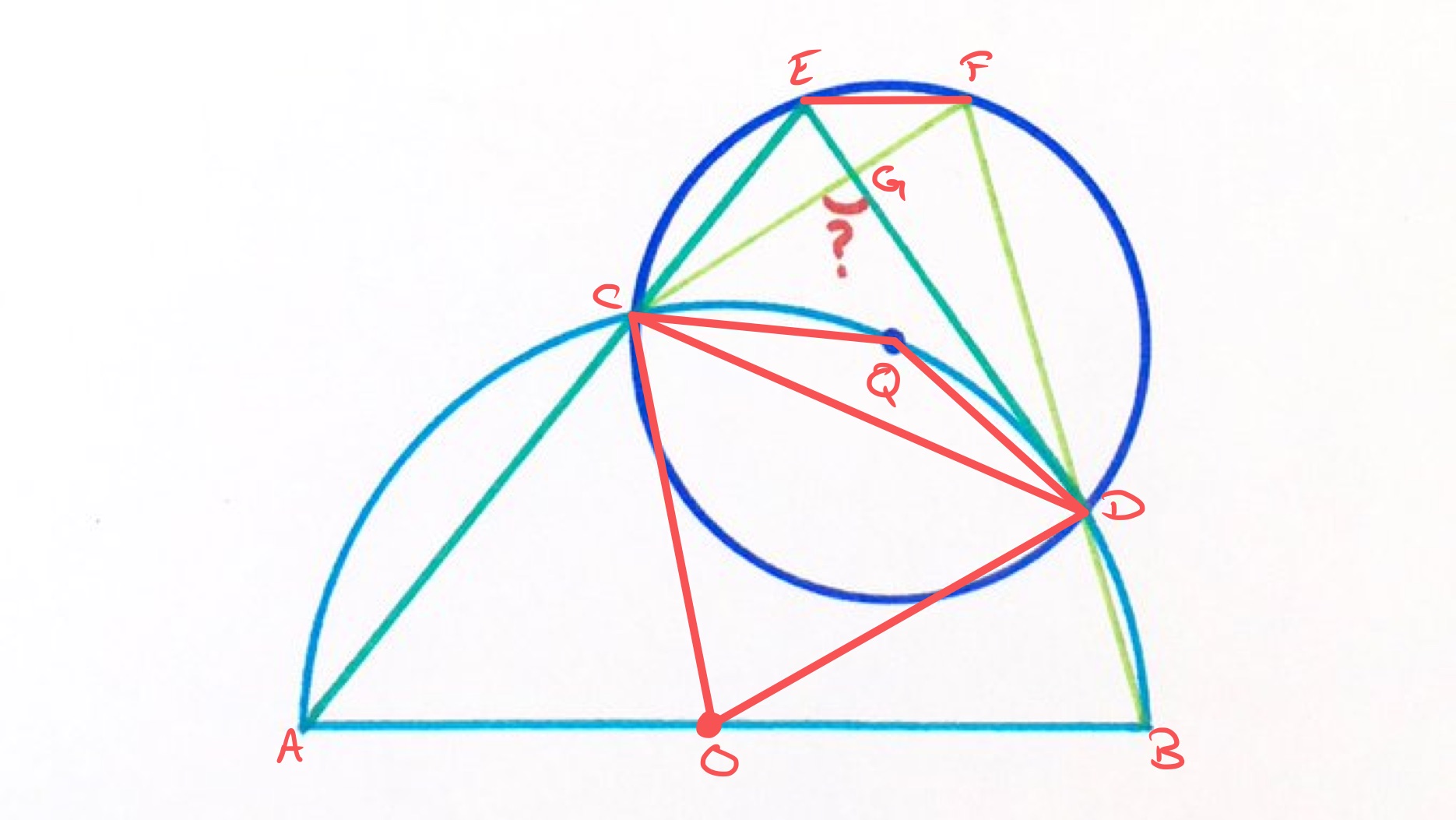
In the above diagram, the point labelled $O$ is the centre of the semi-circle. Let angle $O \hat{A} C$ be $a$ and let $D \hat{B} O$ be $b$.

Since opposite angles in a cyclic quadrilateral add up to $180^\circ$, angles $O \hat{A} C$ and $C \hat{D} B$ add up to $180^\circ$, so angle $C\hat{D} B$ is $180^\circ - a$. Then as angles at a point on a straight line also add up to $180^\circ$, angle $F \hat{D} C$ and $C\hat{D} B$ add up to $180^\circ$, so $F \hat{D}C$ is equal to angle $a$. Using opposite angles in a cyclic quadrilateral again, angles $C \hat{E} F$ and $F \hat{D} C$ add up to $180^\circ$ meaning that angle $C \hat{E} F$ is $180^\circ - a$. A similar argument shows that angle $E \hat{F} D$ is $180^\circ - b$. The sum of angles $C \hat{E} F$ and $E \hat{F} D$ is therefore $360^\circ - a - b$.

As triangle $O C A$ is isosceles and the angles in a triangle add up to $180^\circ$, angle $C \hat{O} A$ is $180^\circ - 2 a$. Using a similar argument gives angle $B \hat{O} D$ as $180^\circ - 2 b$. Therefore the reflex angle $C \hat{O} D$ is $540^\circ - 2a - 2 b$. Since the angle at the centre is twice the angle at the circumference, the reflex angle $C \hat{O} D$ is $270^\circ - a - b$. Applying this again shows that this is twice each of the angles $C \hat{E} D$ and $C \hat{F} D$. So the sum of the angles $C \hat{E} D$ and $C \hat{F} D$ is angle $270^\circ - a - b$.

The sum of angles $G \hat{E} F$ and $E \hat{F} G$ is then the difference between these two sums, so is $90^\circ$. Since the angles in a triangle add up to $180^\circ$, angle $F \hat{G} E$ is $90^\circ$. Therefore as vertically opposite angles are equal, angle $C \hat{G} D$ is $90^\circ$.