Notes
angle formed by three squares solution
Angle Formed by Three Squares
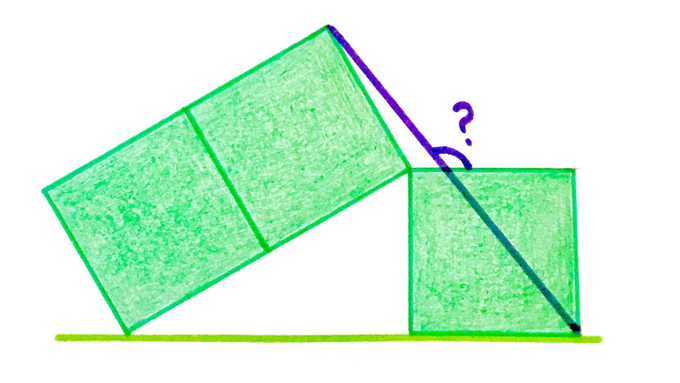
The squares are all the same size. What’s the angle?
Solution by Trigonometry
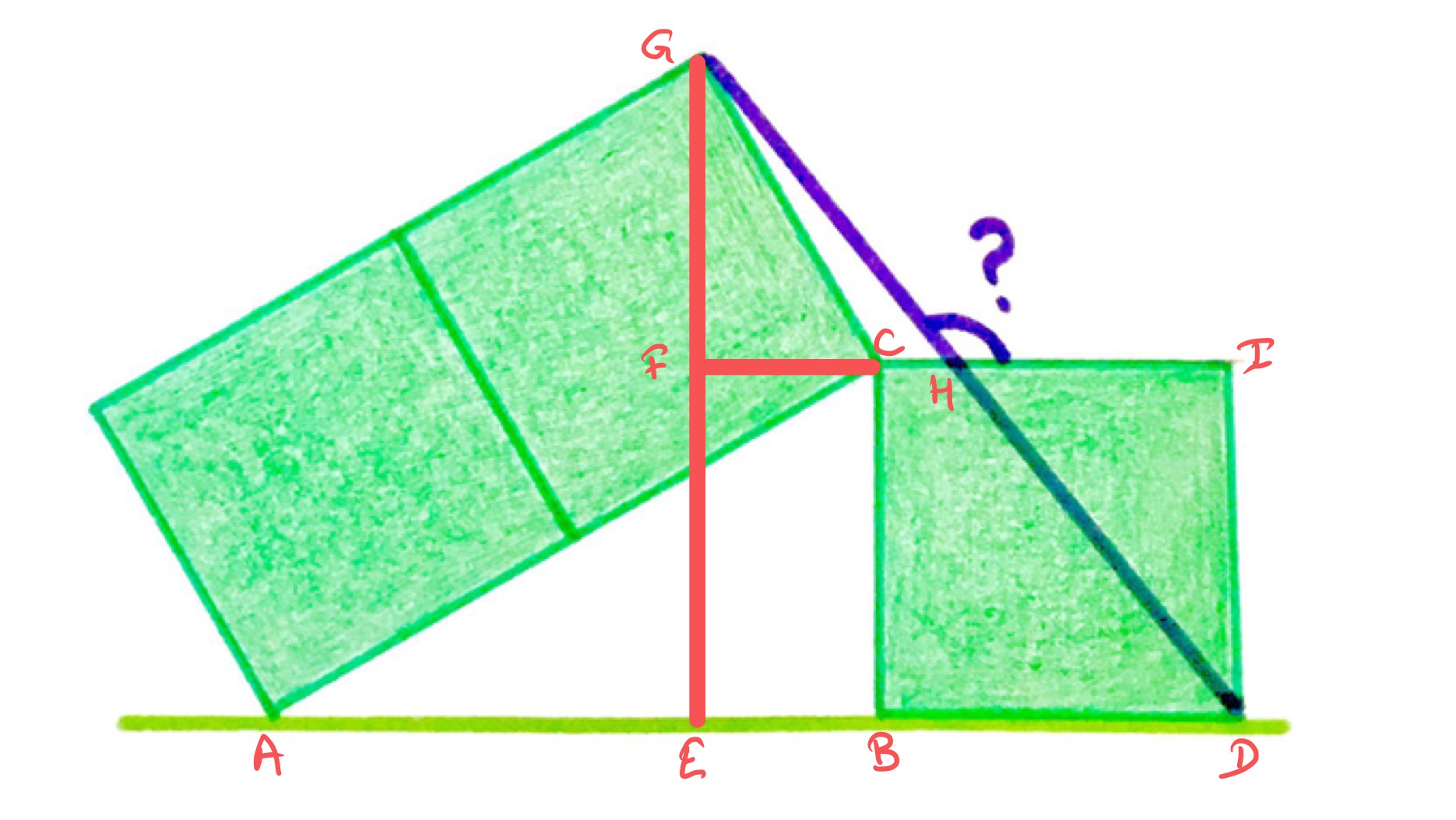
With the points labelled as above, triangle is a right-angled triangle with twice the length of and so is half an equilateral triangle. This means that is also half an equilateral triangle, so if is the length of the side of one square, has length and has length . Then has length and has length . The tangent of angle is therefore:
So to decimal places, angle is: