Notes
angle formed by three rectangles solution
Solution to the Angle Formed by Three Rectangles Puzzle
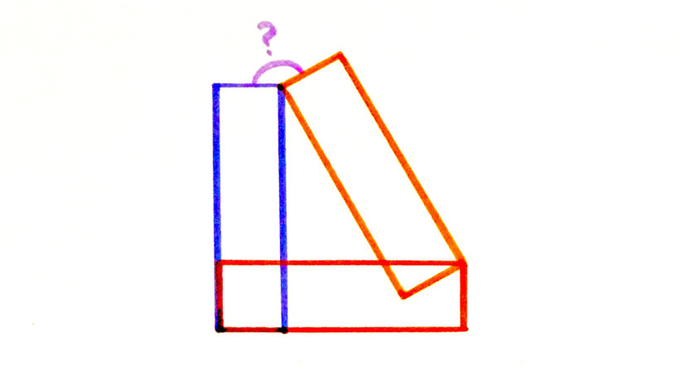
Three congruent rectangles. What’s the angle?
Solution by Triangles
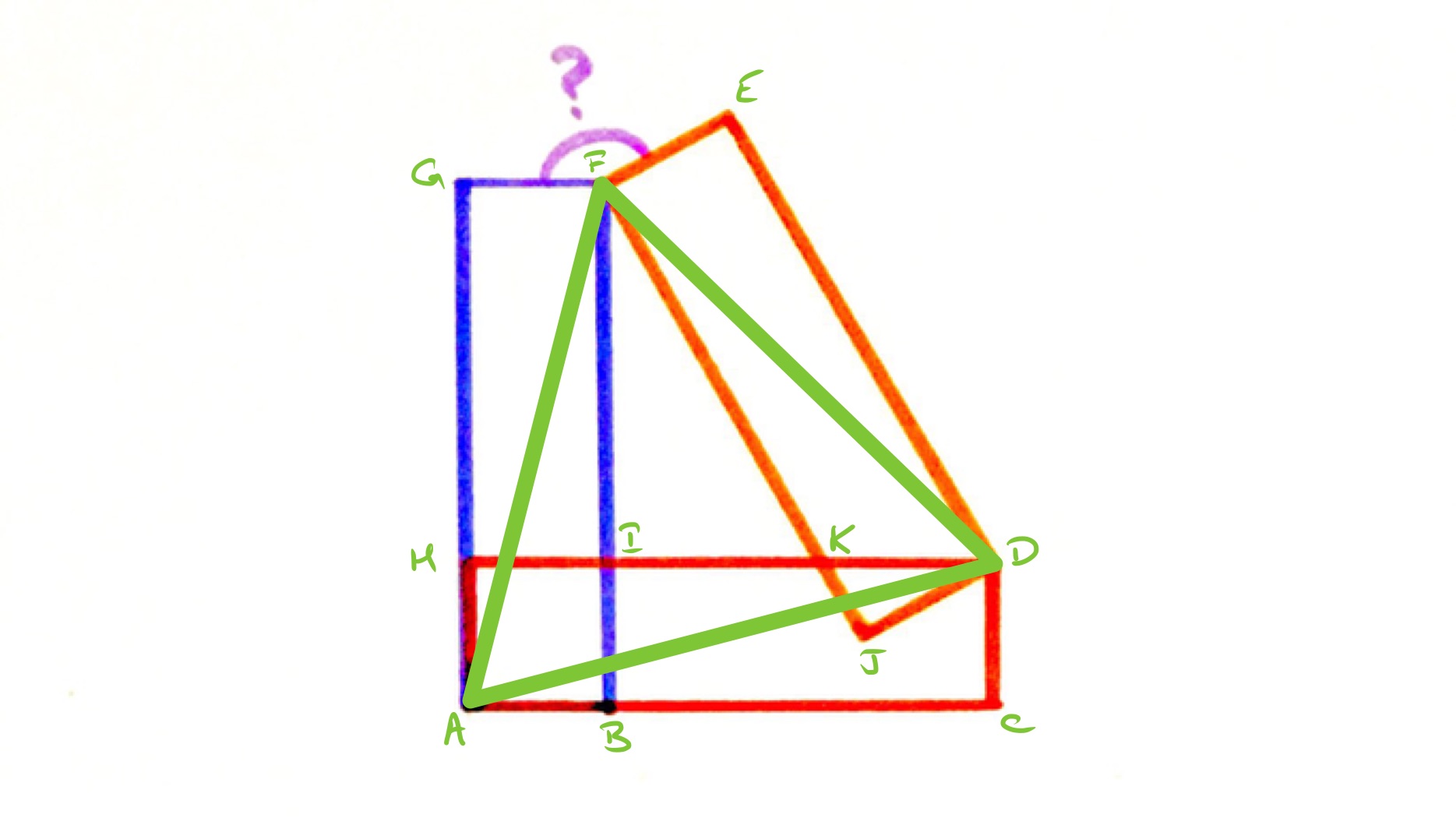
With the points labelled as in the diagram above, the line segments , , and all have the same length since they are diagonals of congruent rectangles. This means that triangle is an equilateral triangle and so angle is . In triangle , angle is and sides and have the same length. Therefore, triangle is an isosceles right-angled triangle so angle is . Putting these together, angle . This is the same as angle and so angle is . Therefore, angle .