Notes
a square in a square solution
Solution to the A Square in a Square Puzzle

The shaded square covers half the larger square. What’s the angle?
Solution by Area of a Triangle and Angles in an Equilateral Triangle
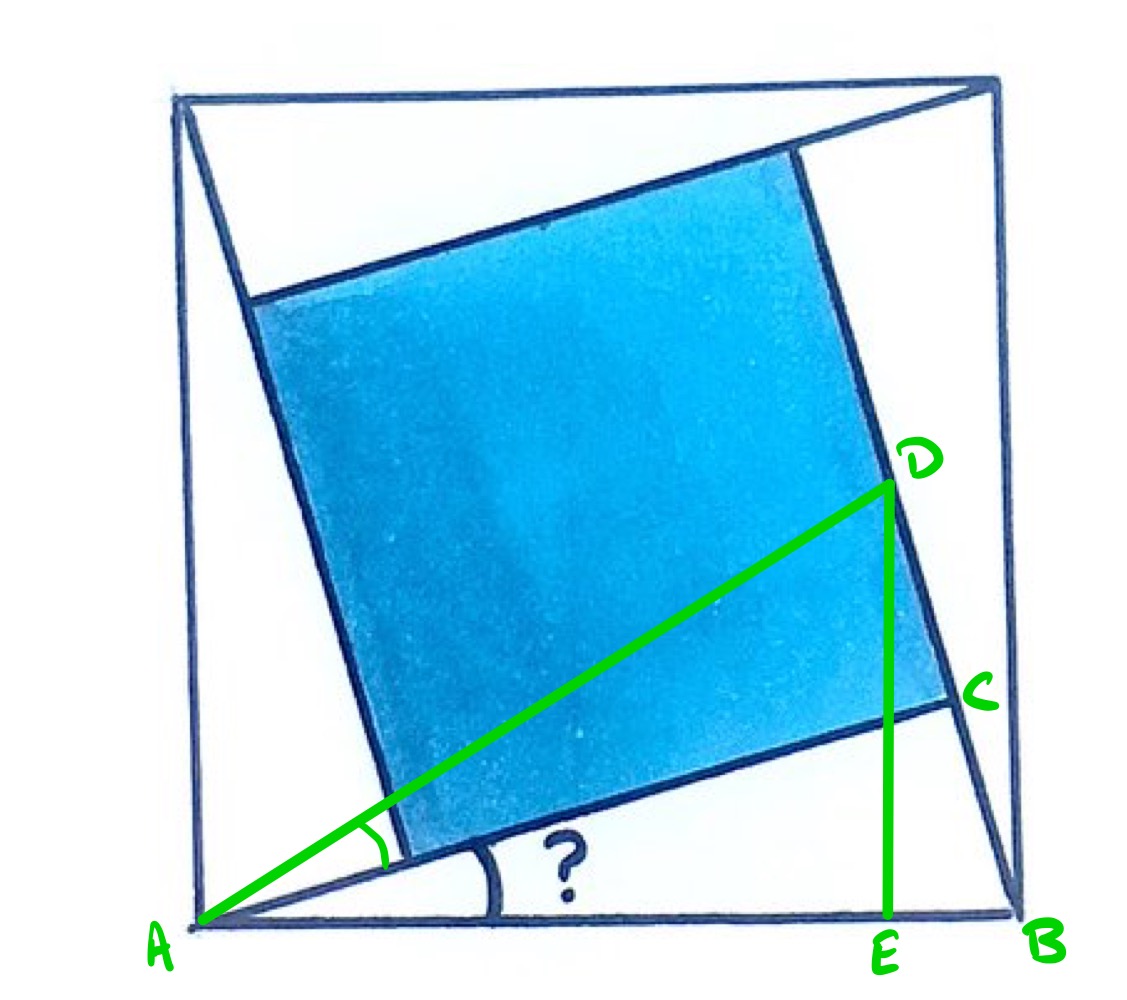
In the above diagram, is the point where and have the same length, and is so that is perpendicular to .
Label the lengths in triangle by , , where is the length of , of , and of . Let be the length of .
Triangle has area , and four of them have half the area of the outer square, so , and thus .
Triangle has twice the area of triangle , so has area . Its area is also . Putting these together shows that .
Since is congruent to , triangle is a right-angled triangle with half the length of , hence it is half of an equilateral triangle and so angle is , meaning that angle is .
Solution by Trigonometry and the Double Angle Formula for Sine
With the lengths as above, let be angle . Then:
As above, so:
Therefore and so .